如图.已知等边三角形ABC中.AG⊥BC.PD⊥BC.PE⊥AC.PF⊥AB．求证:PD+PE+PF=AG．题目和参考答案——青夏教育精英家教网—

题目内容

16．

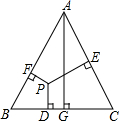如图，已知等边三角形ABC中，AG⊥BC，PD⊥BC，PE⊥AC，PF⊥AB．求证：PD+PE+PF=AG．

分析根据面积相等，又利用△ABC是等边三角形，即可得PE+PD+PF=AG．

解答解：连接PA，PB，PC，
∵S_△ABP+S_△BCP+S_△ACP=S_△ABC，
∴$\frac{1}{2}$AB•PE+$\frac{1}{2}$BC•PD+$\frac{1}{2}$AC•PF=$\frac{1}{2}$BC•AG，
∵△ABC是等边三角形，
∴AB=BC=AC，
∴PE+PD+PF=AG．

点评本题主要考查了等边三角形的性质以及三角形面积的计算方法，熟练掌握等边三角形的性质定理是解题的关键．

练习册系列答案

相关题目

6．

如图，在△ABC中，AC的垂直平分线交AC于E，交BC于D，△ABD的周长为20cm，AE=5cm，则△ABC的周长是30cm．

7．

如图，在△ABC中，BD、CE分别是∠ABC，∠ACB的平分线．
（1）若∠ABC=60°，∠ACB=40°时，求∠BPC的度数．
（2）当∠A=80°时，求∠BPC的度数．
（3）当∠A=x时，用含x代数式表示∠BPC的度数．

4．

如图，在△ABC中，∠C=40°，∠B=80°，AD平分∠CAB，求：
（1）∠1的度数；
（2）求∠ADC的度数．

11．画出函数y=-2x²的图象，并根据图象，求：
（1）x=1，-1.2时y的值；
（2）y=-2，-4时x的坐标（精确到0.1）．

1．

根据数轴，解答下列问题：
（1）点C表示4的相反数，点D的绝对值是0，请在数轴上描出点C，D；
（2）点A向右移动2个单位与哪一点重合？

8．Rt△ABC中，∠C=90°，AC=15，AB=25，则Rt△ABC的面积是150．

5．

如图，已知△ABC的面积为21cm²，CD是△ABC的高，若CD=6cm，则AB=7cm．

6．

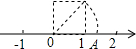数轴上的点并不都表示有理数，如图，以数轴的单位长度为边作正方形，以数轴上的原点O为圆心，正方形的对角线的长为半径画弧，与数轴交于一点A，则点A表示的数为$\sqrt{2}$．

试题分类