题目内容
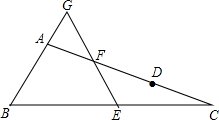 如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.
如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.考点:相似三角形的判定与性质,等腰三角形的判定
专题:
分析:如图,作辅助线,首先运用三角形的中位线定理证明HF=HE,∠HFE=∠HEF;进而证明AG=AF,问题即可解决.
解答: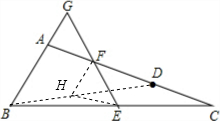 解:△AGF为等腰三角形.
解:△AGF为等腰三角形.
如图,连接BD,取BD的中点H,连接HF、HE;
∵E,F分别为BC,AD的中点,
∴HF∥AB,HE∥CD,且HF=
AB,HE=
CD;
∴∠HFE=∠G,∠HEF=∠AFG;
∵AB=CD,
∴HF=HE,∠HFE=∠HEF;
∴∠G=∠AFG,
∴AG=AF,△AGF为等腰三角形.
 解:△AGF为等腰三角形.
解:△AGF为等腰三角形.如图,连接BD,取BD的中点H,连接HF、HE;
∵E,F分别为BC,AD的中点,
∴HF∥AB,HE∥CD,且HF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠HFE=∠G,∠HEF=∠AFG;
∵AB=CD,
∴HF=HE,∠HFE=∠HEF;
∴∠G=∠AFG,
∴AG=AF,△AGF为等腰三角形.
点评:该题以三角形为载体,以考查三角形的中位线定理、等腰三角形的判定等重要几何知识点为核心构造而成;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
若|a|=2,则a=( )
| A、2 |
| B、-2 |
| C、2 或-2 |
| D、以上答案都不对 |
对下列各式计算结果的符号判断正确的一个是( )
A、(-2)×(-2
| ||||
| B、(-5)-5+1>0 | ||||
C、(-1)+(-
| ||||
| D、(-1)×(-2)<0 |
 如图,BM是△ABC的角平分线,D是BC边上的一点,连接AD,使AD=DC,且∠BAD=120°,则∠AMB=( )
如图,BM是△ABC的角平分线,D是BC边上的一点,连接AD,使AD=DC,且∠BAD=120°,则∠AMB=( )| A、30° | B、25° |
| C、22.5° | D、20° |


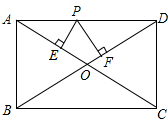 如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为( )
如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为( )