题目内容
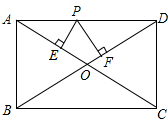 如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为( )
如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为( )| A、10 | B、4.8 | C、6 | D、5 |
考点:矩形的性质,三角形的面积
专题:
分析:连接OP,利用勾股定理列式求出BD,再根据矩形的对角线相等且互相平分求出OA、OD,然后根据S△AOD=S△AOP+S△DOP列方程求解即可.
解答: 解:如图,连接OP,
解:如图,连接OP,
∵AB=6,AD=8,
∴BD=
=
=10,
∵四边形ABCD是矩形,
∴OA=OD=
×10=5,
∵S△AOD=S△AOP+S△DOP,
∴
×6×8=
×5•PE+
×5•PF,
解得PE+PF=4.8.
故选B.
 解:如图,连接OP,
解:如图,连接OP,∵AB=6,AD=8,
∴BD=
| AB2+AD2 |
| 62+82 |
∵四边形ABCD是矩形,
∴OA=OD=
| 1 |
| 2 |
∵S△AOD=S△AOP+S△DOP,
∴
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解得PE+PF=4.8.
故选B.
点评:本题考查了矩形的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键.

练习册系列答案
相关题目
已知a、b为有理数,下列说法中正确的是( )
| A、a2>0 | ||
| B、a3=-a3 | ||
| C、若0<a<1,则a2<a3 | ||
D、若-1<b<0,则b>
|
下列计算错误的是( )
| A、(a-b)(-a-b)=b2-a2 |
| B、(-x-1)2=(x2+2x+1) |
| C、(1+x)(x-1)=x2-1 |
| D、(x-2)(x-3)=x2+x-6 |
 如图,AD是△CAB的角平分线,∠B=34°,∠DAC=30°,则∠ACB的度数是( )
如图,AD是△CAB的角平分线,∠B=34°,∠DAC=30°,则∠ACB的度数是( )| A、96° | B、86° |
| C、76° | D、60° |
观察图中正方形四个顶点所标的数字规律,可知数2014应标在( )


| A、第503个正方形的左下角 |
| B、第503个正方形的右下角 |
| C、第504个正方形的左下角 |
| D、第504个正方形的右上角 |
 一个材质均匀的正方体的六个面分别标有文字“祝、你、天、天、快、乐”,其表面展开图如图所示,随机抛掷这个正方体,“天”字朝上的概率是( )
一个材质均匀的正方体的六个面分别标有文字“祝、你、天、天、快、乐”,其表面展开图如图所示,随机抛掷这个正方体,“天”字朝上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,点A、B、C、D都在⊙O上,若∠A=65°,则∠D=
如图,点A、B、C、D都在⊙O上,若∠A=65°,则∠D=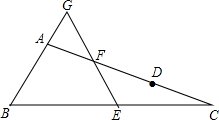 如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.
如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.