题目内容
已知,正方形ABCD与正方形CEFG的位置分别如图①、图②、图③所示,点G在线段CD或CD的延长线上.分别连接BD、BF、FD,得到△BFD.
(1)在图①、图②、图③中,若正方形CEFG的边长分别为1,3,4,且正方形ABCD边长均为3,请通过计算填写下表.
(2)若正方形ABCD的边长为a,正方形CEFG的边长为b,通过(1)中的计算结果猜想△BFD的面积的大小有什么规律,并结合图③说明你的猜想结果的正确性.
(1)在图①、图②、图③中,若正方形CEFG的边长分别为1,3,4,且正方形ABCD边长均为3,请通过计算填写下表.
| 正方形CEFG的边长 | 1 | 3 | 4 |
| △BFD的面积 |

考点:规律型:图形的变化类,三角形的面积
专题:
分析:(1)①图中,利用S△BDF=S△BCD+S梯形EFDC-S△BFE,即可求出△BDF的面积;②直接利用S△BDF=
DF×AB,可求出△BDF的面积;③利用S△BDF=S△BCD+S梯形EFDC-S△BFE,可求出△BDF的面积;
(2)S△BDF=
b2,可利用S△BDF=S△BCD+S梯形EFDC-S△BFE,把a、b代入,化简即可求出△BDF的面积.
| 1 |
| 2 |
(2)S△BDF=
| 1 |
| 2 |
解答:解:(1)填表如下:
 (2)猜想△BFD的面积等于正方形ABCD面积的一半.
(2)猜想△BFD的面积等于正方形ABCD面积的一半.
证明:如图③,连接CF,由正方形性质可知∠DBC=∠FCE=45°,
∴BD∥CF,
∴△BFD与△BCD的BD边上的高相等,
∴S△BFD=S△BCD=
a2.
| 正方形CEFG的边长 | 1 | 3 | 4 |
| △BFD的面积 | 4.5 | 4.5 | 4.5 |
 (2)猜想△BFD的面积等于正方形ABCD面积的一半.
(2)猜想△BFD的面积等于正方形ABCD面积的一半.证明:如图③,连接CF,由正方形性质可知∠DBC=∠FCE=45°,
∴BD∥CF,
∴△BFD与△BCD的BD边上的高相等,
∴S△BFD=S△BCD=
| 1 |
| 2 |
点评:本题考查了图形的变化类问题,利用了面积分割法、正方形的性质、以及同底等高的三角形的面积相等等知识.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
在下列四组数中,不是勾股数的一组数是( )
| A、a=3,b=4,c=5 |
| B、a=15,b=20,c=25 |
| C、a=3,b=5,c=7 |
| D、a=5,b=12,c=13 |
已知a、b为有理数,下列说法中正确的是( )
| A、a2>0 | ||
| B、a3=-a3 | ||
| C、若0<a<1,则a2<a3 | ||
D、若-1<b<0,则b>
|
下列计算错误的是( )
| A、(a-b)(-a-b)=b2-a2 |
| B、(-x-1)2=(x2+2x+1) |
| C、(1+x)(x-1)=x2-1 |
| D、(x-2)(x-3)=x2+x-6 |
观察图中正方形四个顶点所标的数字规律,可知数2014应标在( )


| A、第503个正方形的左下角 |
| B、第503个正方形的右下角 |
| C、第504个正方形的左下角 |
| D、第504个正方形的右上角 |
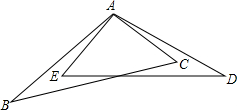 如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是
如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是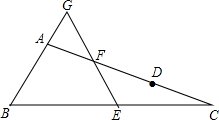 如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.
如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.