题目内容
 如图,BM是△ABC的角平分线,D是BC边上的一点,连接AD,使AD=DC,且∠BAD=120°,则∠AMB=( )
如图,BM是△ABC的角平分线,D是BC边上的一点,连接AD,使AD=DC,且∠BAD=120°,则∠AMB=( )| A、30° | B、25° |
| C、22.5° | D、20° |
考点:等腰三角形的性质,角平分线的定义,三角形的外角性质
专题:
分析:由角平分线可知∠ABM=∠CBM,由DA=DC可得∠C=∠DAC,再利用外角性质和三角形内角和可求得∠CBM+∠C,即∠AMB的度数.
解答:解:∵BM平分∠ABC,
∴∠ABM=∠CBM,
∵AD=DC,
∴∠DAC=∠C,
在△ABC中,∠ABC+∠BAC+∠C=180°,
即2∠CBM+∠BAD+2∠C=180°,且∠BAD=120°
∴∠CBM+∠C=30°,
∴∠AMB=∠CBM+∠C=30°,
故选A.
∴∠ABM=∠CBM,
∵AD=DC,
∴∠DAC=∠C,
在△ABC中,∠ABC+∠BAC+∠C=180°,
即2∠CBM+∠BAD+2∠C=180°,且∠BAD=120°
∴∠CBM+∠C=30°,
∴∠AMB=∠CBM+∠C=30°,
故选A.
点评:本题主要考查等腰三角形的性质及三角形内角和定理、外角的性质,掌握等边对等角是解题的关键,注意方程思想的应用.

练习册系列答案
相关题目
在下列四组数中,不是勾股数的一组数是( )
| A、a=3,b=4,c=5 |
| B、a=15,b=20,c=25 |
| C、a=3,b=5,c=7 |
| D、a=5,b=12,c=13 |
观察图中正方形四个顶点所标的数字规律,可知数2014应标在( )


| A、第503个正方形的左下角 |
| B、第503个正方形的右下角 |
| C、第504个正方形的左下角 |
| D、第504个正方形的右上角 |
下列各数是无理数的是( )
| A、7 | ||
B、
| ||
C、
| ||
D、
|
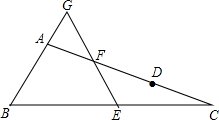 如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.
如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.