题目内容
已知圆锥的侧面展开图的图心角是72°,它的侧面积为5πcm2,则该圆锥的全面积是 cm2.
考点:圆锥的计算,扇形面积的计算
专题:
分析:根据圆锥的侧面展开扇形的侧面积和圆心角的度数求的圆锥的地面半径后即可求的其全面积.
解答:解:设圆锥的母线长为R,
则:
=5π,
解得:R=
cm.
∴底面的周长为l=2S÷R=20π÷
=
π,
∴底面半径为
π÷2π=
cm,
∴底面积为
π,
∴全面积=5π+
π=5.5πcm2.
故答案为5.5π.
则:
| 72πR2 |
| 360 |
解得:R=
5
| ||
| 2 |
∴底面的周长为l=2S÷R=20π÷
5
| ||
| 2 |
| 2 |
∴底面半径为
| 2 |
| ||
| 2 |
∴底面积为
| 1 |
| 2 |
∴全面积=5π+
| 1 |
| 2 |
故答案为5.5π.
点评:本题考查了圆锥的计算,解题的关键是扇形的面积公式为
的灵活运用.
| nπR2 |
| 360 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
小明在解方程时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是2y-
=
y- ,怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=-
,怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=-
.很快就补好了这个常数,这个常数应是( )
| 1 |
| 2 |
| 1 |
| 2 |
 ,怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=-
,怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=-| 7 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
观察图中正方形四个顶点所标的数字规律,可知数2014应标在( )


| A、第503个正方形的左下角 |
| B、第503个正方形的右下角 |
| C、第504个正方形的左下角 |
| D、第504个正方形的右上角 |
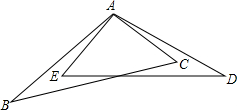 如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是
如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是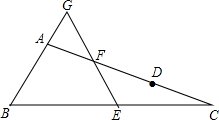 如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.
如图,在△ABC中,AC>AB,D在AC上,AB=CD,E,F分别为BC,AD的中点,连接E,F并延长,与BA延长线交于点G,试判断△AGF的形状,并说明理由.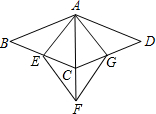 如图,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,AE=2,则AB=
如图,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,AE=2,则AB=