题目内容
5.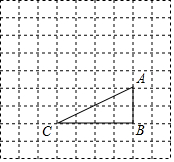 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).(1)在图中标出△ABC外心D的位置,并直接写出它的坐标;
(2)判断△ABC的外接圆D与x轴、y轴的位置关系,并说明理由.
分析 (1)根据A点的坐标建立平面直角坐标系,找出线段AC的中点即为D点;
(2)根据D点坐标即可得出结论.
解答  解:(1)如图,△ABC的外心D点的坐标为(3,2);
解:(1)如图,△ABC的外心D点的坐标为(3,2);
(2)△ABC的外接圆D与x轴相交,与y轴相离,
理由:∵由题意可知△ABC为直角三角形,AB=2,CB=4,
∴斜边即为外接圆的直径,
半径等于$\frac{1}{2}$AC=$\frac{1}{2}$$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{5}$.
又∵外心坐标为(3,2),
∴外心D到x轴的距离为2,到y轴的距离为3,
∵2<$\sqrt{5}$,3>$\sqrt{5}$,
∴△ABC的外接圆D与x轴相交,与y轴相离.
点评 本题考查的是三角形的外接圆与外心,熟知直角三角形的外心为直角三角形斜边的中点是解答此题的关键.

练习册系列答案
相关题目
15. 如图,若l1∥l2,则∠α等于( )
如图,若l1∥l2,则∠α等于( )
 如图,若l1∥l2,则∠α等于( )
如图,若l1∥l2,则∠α等于( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
 如图,AB⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
如图,AB⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.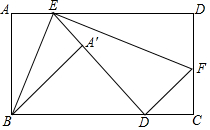 如图,在矩形纸片ABCD中,AB=2,点E在边AD上,沿BE折叠点落在矩形内部的A'处,再把矩形沿EF折叠,使点D落在AC边上的点D'处,旦点E、A'、D'在同一直线上,求AD的最小值.
如图,在矩形纸片ABCD中,AB=2,点E在边AD上,沿BE折叠点落在矩形内部的A'处,再把矩形沿EF折叠,使点D落在AC边上的点D'处,旦点E、A'、D'在同一直线上,求AD的最小值. 如图,P为矩形ABCD内一点,求证:S△PBC=S△PAC+S△PCD.
如图,P为矩形ABCD内一点,求证:S△PBC=S△PAC+S△PCD. 如图,将一个等腰直角三角板按如图方式放置在一个矩形纸片上,其中∠α=20°,则∠β的度数为25°.
如图,将一个等腰直角三角板按如图方式放置在一个矩形纸片上,其中∠α=20°,则∠β的度数为25°.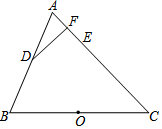 如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F. 如图,矩形ABCD中,AB=5,BC=10,点E是BC上一动点,将△ABE沿AE翻折得到△AEF,当DF=3$\sqrt{5}$时,BE=$\frac{5}{2}$或10.
如图,矩形ABCD中,AB=5,BC=10,点E是BC上一动点,将△ABE沿AE翻折得到△AEF,当DF=3$\sqrt{5}$时,BE=$\frac{5}{2}$或10.