题目内容
17.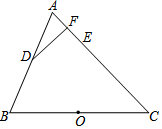 如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)若BC=9,EF=1,求DF的长.
分析 (1)连接OD,证明OD∥AC,即可证得∠ODF=∠AFD=90°,从而证得OD是圆的切线;
(2)过O作OG⊥EC交EC于点G,证得四边形OGFD是矩形,在Rt△OCG中利用勾股定理求得OG,则DF即可求得.
解答 解:(1)DF与⊙O相切.
连接OD.
∵AC=BC,OB=OD,
∴∠B=∠A,∠B=∠1.
∴∠A=∠1.
∴OD∥AC.
∵DF⊥AC,
∴∠AFD=90°.
∴∠ODF=∠AFD=90°.
又∵OD是⊙O的半径,
∴DF与⊙O相切.
(2)过O作OG⊥EC交EC于点G.
∵∠ODF=∠AFD=90°,
∴四边形OGFD是矩形.
∴DF=OG,FG=OD=$\frac{1}{2}$BC=$\frac{9}{2}$.
∵OG⊥EC,
∴CG=EG=FG-EF=$\frac{9}{2}$-1=$\frac{7}{2}$.
∴DF=OG=$\sqrt{O{G}^{2}-C{G}^{2}}$=$\sqrt{(\sqrt{2})^{2}-(\frac{7}{2})^{2}}$=2$\sqrt{2}$.
点评 本题考查了切线的判定与矩形的判定与性质,正确作出辅助线是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
7.下列命题中,是真命题的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 同旁内角互补,两直线平行 | |
| D. | 互补的两个角一定有一个锐角,一个钝角 |
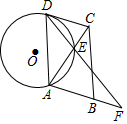 已知,如图,四边形ABCD是平行四边形,⊙O与边DC相切于点D,交对角线AC于点E,连接DE并延长交AB的延长线于点F,且AE=DE.
已知,如图,四边形ABCD是平行四边形,⊙O与边DC相切于点D,交对角线AC于点E,连接DE并延长交AB的延长线于点F,且AE=DE.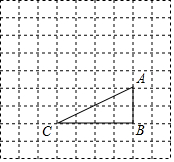 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).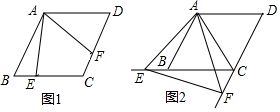
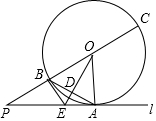 如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.
如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.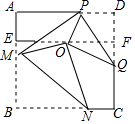 如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$.
如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$.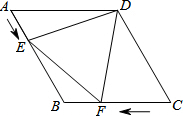 如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )
如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )