题目内容
14. 如图,矩形ABCD中,AB=5,BC=10,点E是BC上一动点,将△ABE沿AE翻折得到△AEF,当DF=3$\sqrt{5}$时,BE=$\frac{5}{2}$或10.
如图,矩形ABCD中,AB=5,BC=10,点E是BC上一动点,将△ABE沿AE翻折得到△AEF,当DF=3$\sqrt{5}$时,BE=$\frac{5}{2}$或10.
分析 分两种情况进行讨论:点F在AD下方;点F在AD上方,分别过F作GH⊥BC于H,交AD于G,先根据勾股定理求得AG=4,GF=3,再根据相似三角形的对应边成比例列式计算,即可得到EF的长,进而由折叠的性质得出BE的长.
解答 解:分两种情况:
①如图,当点F在AD下方时,过F作GH⊥BC于H,交AD于G,则FG⊥AD,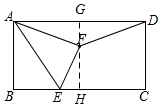
由折叠可得AF=AB=5,
设AG=x,则DG=10-x,
∵AF2-AG2=GF2=DF2-DG2,
∴52-x2=(3$\sqrt{5}$)2-(10-x)2,
解得x=4,
∴AG=4,
∴Rt△AGF中,GF=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴FH=5-3=2,
∵∠AGF=∠FHE=90°=∠AFE,
∴∠GAF=∠HFE,
∴△GAF∽△HFE,
∴$\frac{EF}{FA}$=$\frac{FH}{AG}$,即$\frac{EF}{5}$=$\frac{2}{4}$,
∴EF=$\frac{5}{2}$,
∴BE=FE=$\frac{5}{2}$;
②如图,当点F在AD上方时,过F作FH⊥BC于H,交AD于G,则FG⊥AD,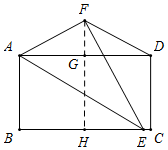
同理可得AG=4,FG=3,
∵GH=AB=5,
∴FH=3+5=8,
∵∠AFE=∠AGF=90°,
∴∠FAG=∠EFH,
又∵∠AGF=∠FHE=90°,
∴△AGF∽△FHE,
∴$\frac{EF}{FA}$=$\frac{HF}{GA}$,即$\frac{EF}{5}$=$\frac{8}{4}$,
∴FE=10,
∴BE=FE=10,
综上所述,BE的长为$\frac{5}{2}$或10.
故答案为:$\frac{5}{2}$或10.
点评 本题主要考查了折叠问题、矩形的性质、勾股定理以及相似三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造直角三角形以及相似三角形,依据勾股定理以及相似三角形的性质进行计算求解.

 阅读快车系列答案
阅读快车系列答案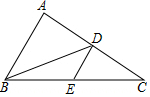 如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为8.
如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为8.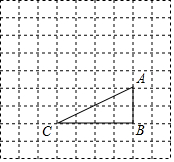 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).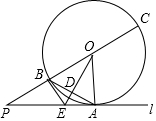 如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.
如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.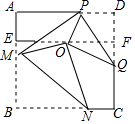 如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$.
如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$. 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.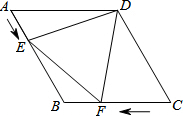 如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )
如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )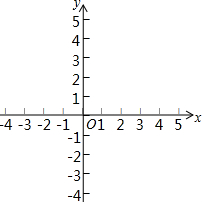 在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).
在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).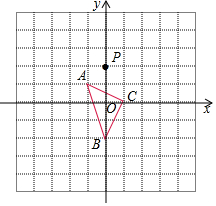 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,1),B(0,-2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为(-2,0).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,1),B(0,-2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为(-2,0).