题目内容
13.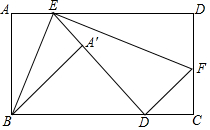 如图,在矩形纸片ABCD中,AB=2,点E在边AD上,沿BE折叠点落在矩形内部的A'处,再把矩形沿EF折叠,使点D落在AC边上的点D'处,旦点E、A'、D'在同一直线上,求AD的最小值.
如图,在矩形纸片ABCD中,AB=2,点E在边AD上,沿BE折叠点落在矩形内部的A'处,再把矩形沿EF折叠,使点D落在AC边上的点D'处,旦点E、A'、D'在同一直线上,求AD的最小值.
分析 如图,作EH⊥BC于H.设AE=x,则易知ED=ED′=BD′,设ED=BDED′=y,在Rt△EHD′中,y2=22+(y-x)2,可得y=$\frac{4+{x}^{2}}{2x}$=$\frac{2}{x}$+$\frac{1}{2}$x,
∴AD=x+y=$\frac{3}{2}$x+$\frac{2}{x}$≥2$\sqrt{\frac{3}{2}x•\frac{2}{x}}$由此即可解决问题.
解答 解: 如图,作EH⊥BC于H.设AE=x,则易知ED=ED′=BD′,设ED=BDED′=y,
如图,作EH⊥BC于H.设AE=x,则易知ED=ED′=BD′,设ED=BDED′=y,
在Rt△EHD′中,y2=22+(y-x)2,
∴y=$\frac{4+{x}^{2}}{2x}$=$\frac{2}{x}$+$\frac{1}{2}$x,
∴AD=x+y=$\frac{3}{2}$x+$\frac{2}{x}$≥2$\sqrt{\frac{3}{2}x•\frac{2}{x}}$,(a+b≥2$\sqrt{ab}$,a>0,b>0)
∴AD≥2$\sqrt{3}$,
∴AD的最小值为2$\sqrt{3}$.
点评 本题考查翻折变换、勾股定理、矩形的性质、不等式的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,记住a+b≥2$\sqrt{ab}$,a>0,b>0,这个基本不等式.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为8.
如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为8.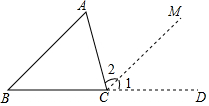 完成下列推理过程
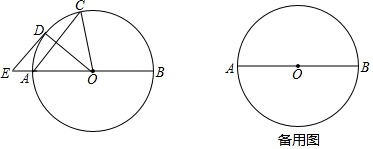
完成下列推理过程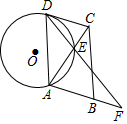 已知,如图,四边形ABCD是平行四边形,⊙O与边DC相切于点D,交对角线AC于点E,连接DE并延长交AB的延长线于点F,且AE=DE.
已知,如图,四边形ABCD是平行四边形,⊙O与边DC相切于点D,交对角线AC于点E,连接DE并延长交AB的延长线于点F,且AE=DE.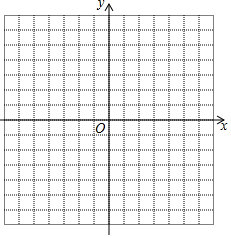 有这样一个问题:探究方程x3-x-2=0的实数根的个数.
有这样一个问题:探究方程x3-x-2=0的实数根的个数.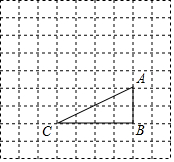 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).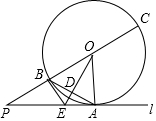 如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.
如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E. 在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).
在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).