题目内容
19.计算(1)x4•(-x3)2÷(-x)3
(2)$(-\frac{1}{2})^{3}+2×{2}^{-3}×{2}^{2}-(-8)^{2007}×(0.125)^{2006}$
(3)(3a-b)2(3a+b)2
(4)(3m-2b+5)(3m+2b-5)
分析 (1)先进行幂的乘方运算,然后进行同底数幂乘除运算;
(2)先乘方运算,然后进行加减运算;
(3)根据平方差公式进行计算;
(4)把(2b-5)看成一个整体,利用平方差公式进行计算.
解答 解:(1)原式=x4•x6•$\frac{-1}{{x}^{3}}$
=-x7 ;
(2)原式=-23 +2×$\frac{1}{8}$×4-(-8)2007×($\frac{1}{8}$)2006
=-8+1+8
=1;
(3)原式=[(3a-2b)(3a+2b)]2
=(9a2-4b2)2
=81a4-18a2b2+b4;
(4)原式=[3m-(2b-5)][3m+(2b-5)]
=9m2-(2b-5)2
=9m2-(4b2-20b+25)
=9m2-4b2+20b-25.
点评 本题主要考查了整式的混合运算以及负整数指数幂的知识,解答本题的关键是掌握平方差公式以及完全平方式以及同底数幂乘除法的运算法则,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图,∠3+∠4=180°,∠2=135°,则∠1度数是( )
如图,∠3+∠4=180°,∠2=135°,则∠1度数是( )
 如图,∠3+∠4=180°,∠2=135°,则∠1度数是( )
如图,∠3+∠4=180°,∠2=135°,则∠1度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
11.已知两条线段长分别为3、4,那么能与它们组成直角三角形的第三条线段长是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 不能确定 |
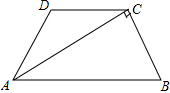 如图,在等腰梯形ABCD中,AB∥CD,AC⊥BC,∠B=60°,AB=6,则CD的长是3.
如图,在等腰梯形ABCD中,AB∥CD,AC⊥BC,∠B=60°,AB=6,则CD的长是3. 如图,在长为4x+3,宽为3x+5的长方形纸片中剪去两个边长分别为-2x+1,x+2的正方形,求阴影部分的面积.
如图,在长为4x+3,宽为3x+5的长方形纸片中剪去两个边长分别为-2x+1,x+2的正方形,求阴影部分的面积. 如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.同时转动两个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作m,将B转盘指针指向的数字记作n.
如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.同时转动两个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作m,将B转盘指针指向的数字记作n.