题目内容
20.点O是△ABC的外心,点I是△ABC的内心,若∠BIC=145°,则∠BOC的度数为( )| A. | 110° | B. | 125° | C. | 130° | D. | 140° |
分析 因为点I为△ABC的内心,推出∠IAB+∠IBA=$\frac{1}{2}$(∠ABC+∠ACB)=180°-145°=35°,推出∠ABC+∠ACB=70°,推出∠A=180°-(∠ABC+∠ACB)=110°,作△ABC的外接圆如图,在⊙O上取一点D,连接BD、CD.因为∠D=180°-∠A=70°,根据∠BOC=2∠D即可解决问题.
解答 解:∵点I为△ABC的内心,
∴∠IAB+∠IBA=$\frac{1}{2}$(∠ABC+∠ACB)=180°-145°=35°,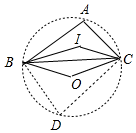
∴∠ABC+∠ACB=70°,
∴∠A=180°-(∠ABC+∠ACB)=110°
∵点O为△ABC的外心,作△ABC的外接圆如图,在⊙O上取一点D,连接BD、CD.
∴∠D=180°-∠A=70°,
∴∠BOC=2∠D=140°.
故选D.
点评 本题主要考查了三角形的内心与外心,正确得出∠A的度数是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.一列动车以300km/h的速度过第一、第二两个隧道,已知第二个隧道的长度比第一个隧道长度的2倍还多1.5km,已知该列动车过第二个隧道比第一个隧道多用了93秒,若设第一个隧道的长度为x km,则由题意列出的方程正确的是( )
| A. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-93 | B. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+93 | ||
| C. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-$\frac{93}{3600}$ | D. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+$\frac{93}{3600}$ |
11. 如图,若AB∥CD,则∠A=104°,∠AED=86°,则∠D等于( )
如图,若AB∥CD,则∠A=104°,∠AED=86°,则∠D等于( )
 如图,若AB∥CD,则∠A=104°,∠AED=86°,则∠D等于( )
如图,若AB∥CD,则∠A=104°,∠AED=86°,则∠D等于( )| A. | 10° | B. | 12° | C. | 16° | D. | 18° |
8.已知P=3ax-8x+1,Q=x-2ax-3,无论x取何值时,3P-2Q=9恒成立,则a的值为( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
5.下列事件中属于不可能事件的为( )
| A. | 掷一枚硬币10次,有10次正面朝上 | |
| B. | 任意画一个三角形,其内角和是360° | |
| C. | 汽车经过城市中一段路,途径5个交通信号灯的路口,经过时没遇上红灯 | |
| D. | 掷骰子100次,有100次点数是6的面朝上 |
12.在数轴上表示不等式2(x-1)>-4的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
9.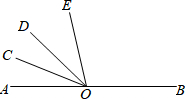 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=α,则∠BOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=α,则∠BOE的度数为( )
 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=α,则∠BOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=α,则∠BOE的度数为( )| A. | 360°-4α | B. | 180°-4α | C. | α | D. | 270°-3α |
 如图,在Rt△ABO 中,AO=4,BO=3,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s).
如图,在Rt△ABO 中,AO=4,BO=3,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s).