题目内容
10.一列动车以300km/h的速度过第一、第二两个隧道,已知第二个隧道的长度比第一个隧道长度的2倍还多1.5km,已知该列动车过第二个隧道比第一个隧道多用了93秒,若设第一个隧道的长度为x km,则由题意列出的方程正确的是( )| A. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-93 | B. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+93 | ||
| C. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-$\frac{93}{3600}$ | D. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+$\frac{93}{3600}$ |
分析 设第一个隧道的长度为xkm,则第二个隧道的长度为(2x+1.5)km,根据该列动车过第二个隧道比第一个隧道多用了93秒列出方程即可.
解答 解:设第一个隧道的长度为xkm,则第二个隧道的长度为(2x+1.5)km,
根据题意,得$\frac{x}{300}$=$\frac{2x+1.5}{300}$-$\frac{93}{3600}$,
故选C.
点评 本题考查由实际问题抽象出一元一次方程,解题的关键是明确题意,抓住关键描述语,找出等量关系.注意单位要统一.

练习册系列答案
相关题目
1.方程x2-2=0的解为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 2或-2 | D. | $\sqrt{2}$或-$\sqrt{2}$ |
5.四边形的两条对角线的长分别是12cm和10cm,顺次连接各边中点所得的新四边形的周长是( )
| A. | 12cm | B. | 22cm | C. | 18cm | D. | 26cm |
15. 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两只等腰直角三角形纸片的面积都为m,另两张直角三角形纸片的面积都为n,中间一张正方形纸片的面积为1,则这个平行四边形的面积一定可以表示为( )
如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两只等腰直角三角形纸片的面积都为m,另两张直角三角形纸片的面积都为n,中间一张正方形纸片的面积为1,则这个平行四边形的面积一定可以表示为( )
 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两只等腰直角三角形纸片的面积都为m,另两张直角三角形纸片的面积都为n,中间一张正方形纸片的面积为1,则这个平行四边形的面积一定可以表示为( )
如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两只等腰直角三角形纸片的面积都为m,另两张直角三角形纸片的面积都为n,中间一张正方形纸片的面积为1,则这个平行四边形的面积一定可以表示为( )| A. | 4m | B. | 4n | C. | 4n+1 | D. | 3m+4 |
2.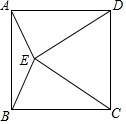 如图,在正方形ABCD的内部作等边△CDE,连接AE,则∠DAE的度数为( )
如图,在正方形ABCD的内部作等边△CDE,连接AE,则∠DAE的度数为( )
 如图,在正方形ABCD的内部作等边△CDE,连接AE,则∠DAE的度数为( )
如图,在正方形ABCD的内部作等边△CDE,连接AE,则∠DAE的度数为( )| A. | 80° | B. | 75° | C. | 70° | D. | 60° |
19.下列事件中,是随机事件的是( )
| A. | 拔苗助长 | B. | 守株待兔 | C. | 水中捞月 | D. | 瓮中捉鳖 |
20.点O是△ABC的外心,点I是△ABC的内心,若∠BIC=145°,则∠BOC的度数为( )
| A. | 110° | B. | 125° | C. | 130° | D. | 140° |

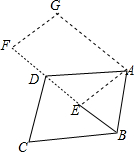 如图,将平行四边形ABCD绕点A顺时针旋转,其中B、C、D分别落在点E,F、G处,且点B、E、D、F在一直线上,若CD=4,BC=2$\sqrt{7}$,则平行四边形ABCD的面积为8$\sqrt{2}$.
如图,将平行四边形ABCD绕点A顺时针旋转,其中B、C、D分别落在点E,F、G处,且点B、E、D、F在一直线上,若CD=4,BC=2$\sqrt{7}$,则平行四边形ABCD的面积为8$\sqrt{2}$.