Question

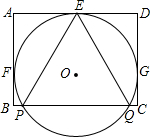如图，⊙O与矩形ABCD的AD、AB、CD的三边分别相切于E、F、G三点，边BC与⊙O交于P、Q两点，若AD=4，AB=3，则sin∠PEQ的值为（　　）

• A、

  2

  2

• B、

  3

  2

• C、

  7

  3

• D、

  4

  5

Answer 1

考点：切线的性质,勾股定理,矩形的性质,垂径定理,锐角三角函数的定义

专题：计算题

分析：连接EO并延长，交圆O于点M，连接FG，过圆心O，连接OP，OQ，由圆O与矩形三边都相切，利用切线的性质得到OE垂直于AD，OF垂直于AB，OG垂直于DC，切线长AE=AF，DE=DG，同时得到四边形AEMB为矩形，四边形AEOF与EODG都为正方形，可得出AE=DE，AD即为圆的直径，求出圆的半径OP的长，再由EM-EO求出OM的长，由OM垂直于PQ，得到M为PQ的中点，在直角三角形OPM中，由OM等于OP的一半，得到∠OPM=30°，进而求出∠POM=60°，又三角形OPQ为等腰三角形，利用三线合一得到OM为∠POQ角平分线，确定出∠POQ的度数，利用同弧所对的圆心角等于所对圆周角的2倍，求出∠PEQ的度数，利用特殊角的三角函数值即可求出所求式子的值．

解答：解：连接EO并延长，交圆O于点M，连接FG，过圆心O，连接OP，OQ，
∵⊙O与矩形ABCD的AD、AB、CD的三边分别相切于E、F、G三点，
∴OE⊥AD，OF⊥AB，OG⊥DC，AE=AF，DE=DG，
∴四边形ABME为矩形，四边形AEOF和EODG为正方形，
∴EM⊥PQ，AE=DE，
∴M为PQ的中点，
又∵AD=4，AB=3，
∴EM=AB=3，FG=AD=4，即圆的直径为4，
∴OP=OE=2，OM=EM-OE=3-2=1，
在Rt△OPM中，OM=

1

2

OP，
∴∠OPM=30°，∠POM=60°，
∴∠POQ=120°，
∴∠PEQ=60°，
则sin∠PEQ=sin60°=

3

2

．
故选B．

点评：此题考查了切线的性质，勾股定理，垂径定理，矩形的性质，等腰三角形的性质，以及特殊角的三角函数值，熟练掌握定理及性质是解本题的关键．