题目内容
将数码1,2,3,4,5,6,7,8,9按某种顺序写成一个九位数
,令A=
+
+
+
+
+
+
,则A的最大可能值为 .
. |
| abcdefghi |
. |
| abc |
. |
| bcd |
. |
| cde |
. |
| def |
. |
| efg |
. |
| fgh |
. |
| ghi |
考点:数的十进制
专题:
分析:假设前9个数字是a、b、c、d、e、f、g、h、i;那么在所有连续三位数相加的等式中a出现1次,b出现2次,c出现3次…g出现3次,h出现2次,i出现1次;那么要使值最大,那么数字最小的数字尽可能的出现的次数少.据此安排1--9的位置,进而求出问题的答案.
解答:解:假设前9个数字是a、b、c、d、e、f、g、h、i;
那么在所有连续三位数相加的等式中a出现1次,b出现2次,c出现3次…g出现3次,h出现2次,i出现1次;
那么要使值最大,那么数字最小的数字尽可能的出现的次数少,
所有1、2 被安排在最后,2在倒数第2个数字,1在最后一个数字,
其次是3、4,4在第2个数字,3在第1个数字;
那么其他的数字均出现了3次,分别在百位、十位、个位出现一次,
相加的值为:
100×(5+6+7+8+9)+10×(5+6+7+8+9)+5+6+7+8+9,
=100×35+10×35+35,
=(100+10+1)×35,
=3885;
最大值为:
3885+3×100+4×100+4×10+2×10+2+1,
=3885+300+400+40+20+3,
=4648.
答:最大可能的值是4648.
故答案为:4648.
那么在所有连续三位数相加的等式中a出现1次,b出现2次,c出现3次…g出现3次,h出现2次,i出现1次;
那么要使值最大,那么数字最小的数字尽可能的出现的次数少,
所有1、2 被安排在最后,2在倒数第2个数字,1在最后一个数字,
其次是3、4,4在第2个数字,3在第1个数字;
那么其他的数字均出现了3次,分别在百位、十位、个位出现一次,
相加的值为:
100×(5+6+7+8+9)+10×(5+6+7+8+9)+5+6+7+8+9,
=100×35+10×35+35,
=(100+10+1)×35,
=3885;
最大值为:
3885+3×100+4×100+4×10+2×10+2+1,
=3885+300+400+40+20+3,
=4648.
答:最大可能的值是4648.
故答案为:4648.
点评:考查了数的十进制,此题也可这样来理解:既然要连续3个数码组成的和最大,9用的次数最多,其次是8、7等.头尾两个只用到1次,然后第二个数码和倒数第二个数码都是放2次的,那么很显然用1、2、3、4,还要考虑和最大,尽量将3、4放在能增大数的百位上,其余的位置都是用到3次的,要最大的话,9在第3位,然后是8、7…,结果这个9位数是349876521,最大的和是349+498+987+876+765+652+521=4648.

练习册系列答案
相关题目
下列命题中,正确的是( )
A、Rt△ABC中,如果CD是AB上中线,那么CD=
| ||
B、Rt△ABC中,如果∠B=30°,那么AC=
| ||
| C、如果点P在∠AOB的平分线上,点M、N分别在OA、OB上,那么PM=PN | ||
| D、如果点P在MN的垂直平分线上,那么PM=PN |
 已知在△ABC中,∠B=30°,tanC=2,AB=2,求△ABC的周长.(结果保留根号)
已知在△ABC中,∠B=30°,tanC=2,AB=2,求△ABC的周长.(结果保留根号)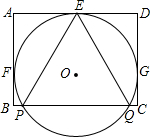 如图,⊙O与矩形ABCD的AD、AB、CD的三边分别相切于E、F、G三点,边BC与⊙O交于P、Q两点,若AD=4,AB=3,则sin∠PEQ的值为( )
如图,⊙O与矩形ABCD的AD、AB、CD的三边分别相切于E、F、G三点,边BC与⊙O交于P、Q两点,若AD=4,AB=3,则sin∠PEQ的值为( ) 如图,等腰△ABC中,AB=AC=10,AB的垂直平分线MN分别交AB于点M,AC于点N,△BCN的周长为16,那么BC=
如图,等腰△ABC中,AB=AC=10,AB的垂直平分线MN分别交AB于点M,AC于点N,△BCN的周长为16,那么BC=
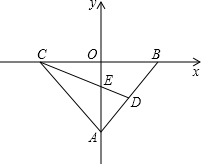 如图所示,在直角坐标系xOy中,点A在y轴负半轴上,点B、C分别在x轴正、负半轴上,AO=8,AB=AC,sin∠ABC=
如图所示,在直角坐标系xOy中,点A在y轴负半轴上,点B、C分别在x轴正、负半轴上,AO=8,AB=AC,sin∠ABC=