题目内容
 把1000以内从1开始的自然数排列成右图,用正方形框往上下左右相邻的4个数.
把1000以内从1开始的自然数排列成右图,用正方形框往上下左右相邻的4个数.(1)设所框住的4个数中最小的一个数为 x,那么另外3个数按从小到大的顺序用含x的代数式可以分别表示为
(2)要使所框住的4个数的和等于:①1000 ②2014,问是否能得到?如果能得到,求出方框中的最大数;如果不能得到,说明理由.
考点:一元一次方程的应用
专题:
分析:(1)根据每行右边一个数比左边的一个数大1,每列中上面一个数比下面的一个数大5,即可表示另外3个数;
(2)①令x+x+1+x+5+x+6=1000,求出x的值,进而作出判断;
②令x+x+1+x+5+x+6=1000,求出x的值,进而作出判断.
(2)①令x+x+1+x+5+x+6=1000,求出x的值,进而作出判断;
②令x+x+1+x+5+x+6=1000,求出x的值,进而作出判断.
解答:解:(1)设所框住的4个数中最小的一个数为 x,那么另外3个数按从小到大的顺序用含x的代数式可以分别表示为 x+1,x+5,x+6.
(2)①依题意有x+x+1+x+5+x+6=1000,
解得x=252,
x+6=258.
答:方框中的最大数是258.
②依题意有x+x+1+x+5+x+6=2014,
解得x=500.5,
∵x为整数,
∴x=500.5不合题意舍去.
故答案为:x+1,x+5,x+6.
(2)①依题意有x+x+1+x+5+x+6=1000,
解得x=252,
x+6=258.
答:方框中的最大数是258.
②依题意有x+x+1+x+5+x+6=2014,
解得x=500.5,
∵x为整数,
∴x=500.5不合题意舍去.
故答案为:x+1,x+5,x+6.
点评:本题主要考查了一元一次方程组的应用,解答本题的关键是掌握左右每行两个数相差1,上下每列两个数相差5,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
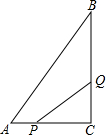 如图所示,在△ABC中,∠C=90°,AC=5cm,BC=7cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=5cm,BC=7cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.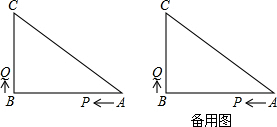 到达点A时,P、Q两点同时停止运动,它们同时出发,设出发的时间为t秒.
到达点A时,P、Q两点同时停止运动,它们同时出发,设出发的时间为t秒.