题目内容
11. 如图,在“2016亚洲足球俱乐部冠军联赛”的一场比赛中,北京国安队的邵佳一带球向对方球门PQ进攻,当他带球冲到A点时,队友徐云龙已经冲到B点,第一种:自己直接射门;第二种:将球传给徐云龙射门,仅从射门角度考虑,应选择第二种射门方式更容易成功.
如图,在“2016亚洲足球俱乐部冠军联赛”的一场比赛中,北京国安队的邵佳一带球向对方球门PQ进攻,当他带球冲到A点时,队友徐云龙已经冲到B点,第一种:自己直接射门;第二种:将球传给徐云龙射门,仅从射门角度考虑,应选择第二种射门方式更容易成功.
分析 本题实际是求∠A和∠B度数的大小;可设AP与⊙O的交点为C,连接QC,由圆周角定理可得∠PCQ=∠B;由于∠PCQ是△ACQ的外角,显然∠PCQ即∠B的度数要大于∠A;因此从射门角度考虑,在B点射门时,射门的角度更大,更有利于进球.
解答 解:如图,
设AP与圆的交点是C,连接CQ;
则∠PCQ>∠A;
由圆周角定理知:∠PCQ=∠B;
所以∠B>∠A;
因此选择第二种射门方式更.
故答案为:二
点评 此题实际上是比较两个角的大小,角度越大,射中率越高.综合考查了圆周角定理和三角形外角的性质.

练习册系列答案
相关题目
2. 如图,在周长为10m的长方形窗户上钉一块宽为1m的长方形遮阳布,使透光部分正好是一正方形,则钉好后透光面积为( )
如图,在周长为10m的长方形窗户上钉一块宽为1m的长方形遮阳布,使透光部分正好是一正方形,则钉好后透光面积为( )
 如图,在周长为10m的长方形窗户上钉一块宽为1m的长方形遮阳布,使透光部分正好是一正方形,则钉好后透光面积为( )
如图,在周长为10m的长方形窗户上钉一块宽为1m的长方形遮阳布,使透光部分正好是一正方形,则钉好后透光面积为( )| A. | 4m2 | B. | 9m2 | C. | 16m2 | D. | 25m2 |
6.已知${(\frac{1}{2}x-k)^2}=\frac{1}{4}{x^2}+x+1$,则k的值为( )
| A. | ±1 | B. | ±2 | C. | -1 | D. | +1 |
16. 如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是( )
如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是( )
 如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是( )
如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是( )| A. | 60° | B. | 80° | C. | 100° | D. | 120° |
3.长方形的一边长为4,对角线与长方形另外一条边相差2,则长方形的面积为( )
| A. | 8 | B. | 4 | C. | 6 | D. | 12 |
20.若-$\frac{a}{2}$<-$\frac{a}{3}$,则a一定满足是( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
1.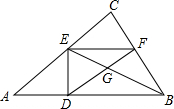 如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )
如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )
 如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )
如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )| A. | t=$\frac{14}{17}$ | B. | t=$\frac{12}{10}$ | C. | t=$\frac{10}{17}$ | D. | t=$\frac{8}{17}$ |
 如图,在平面直角坐标系xOy中,直线l:y=kx-3k(k<0)与x、y轴的正半轴分别交于点A、B,动点D(异于点A、B)在线段AB上,DC⊥x轴于C.
如图,在平面直角坐标系xOy中,直线l:y=kx-3k(k<0)与x、y轴的正半轴分别交于点A、B,动点D(异于点A、B)在线段AB上,DC⊥x轴于C.