题目内容
 已知在△ABC中,∠A=90°,AD⊥BC于点D,M为AD中点,BM的延长线交AC于点P,PQ⊥BC于Q.求证:PQ2=PA•PC.
已知在△ABC中,∠A=90°,AD⊥BC于点D,M为AD中点,BM的延长线交AC于点P,PQ⊥BC于Q.求证:PQ2=PA•PC.考点:相似三角形的判定与性质
专题:证明题
分析:如图,作辅助线;首先证明A、Q、C、N四点共圆,得到PA•PC=PQ•PN;证明△ABM∽△NBP,△DBM∽△QBP,列出比例式,证明PN=PQ;问题即可解决.
解答: 证明:如图,分别延长BA、QP,交于点N;连接CN;
证明:如图,分别延长BA、QP,交于点N;连接CN;
∵∠A=90°,AD⊥BC于点D,
∴∠NAC=∠NQC=90°,
∴A、Q、C、N四点共圆,
∴PA•PC=PQ•PN(相交弦定理),
∵AD⊥BC,PQ⊥BC,
∴AD∥NQ,
∴△ABM∽△NBP,△DBM∽△QBP,
∴AM:PN=BM:BP,DM:PQ=BM:BP,
∴AM:PN=DM:PQ,而AM=DM,
∴PN=PQ,
∴PQ2=PA•PC.
 证明:如图,分别延长BA、QP,交于点N;连接CN;
证明:如图,分别延长BA、QP,交于点N;连接CN;∵∠A=90°,AD⊥BC于点D,
∴∠NAC=∠NQC=90°,
∴A、Q、C、N四点共圆,
∴PA•PC=PQ•PN(相交弦定理),
∵AD⊥BC,PQ⊥BC,
∴AD∥NQ,
∴△ABM∽△NBP,△DBM∽△QBP,
∴AM:PN=BM:BP,DM:PQ=BM:BP,
∴AM:PN=DM:PQ,而AM=DM,
∴PN=PQ,
∴PQ2=PA•PC.
点评:该题在主要考查了相似三角形的判定及其性质应用的同时,还渗透了对四点共圆、相交弦定理等其它几何知识点的考查;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
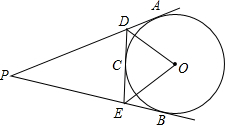 如图,P是圆O外的一点,PA、PB与圆O分别相切于点A、B,C是劣弧
如图,P是圆O外的一点,PA、PB与圆O分别相切于点A、B,C是劣弧 |
| AB |
| A、38° | B、52° |
| C、70° | D、71° |
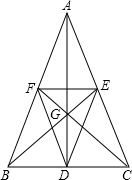 如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.
如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由. 如图,B是AC的中点,D是CE中点.试说明:BD=
如图,B是AC的中点,D是CE中点.试说明:BD=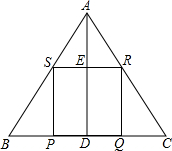 如图,在等腰△ABC中,底边BC=12cm,高AD=8cm,四边形PQRS是正方形.
如图,在等腰△ABC中,底边BC=12cm,高AD=8cm,四边形PQRS是正方形.