题目内容
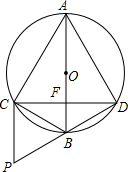 若AC=AD,∠CAD=60°,AB与CD相交于点F,AF=
若AC=AD,∠CAD=60°,AB与CD相交于点F,AF=| 8 |
| 5 |
| 3 |
考点:相似三角形的判定与性质,等边三角形的判定与性质,圆周角定理
专题:
分析:证明△ACD是等边三角形,得到∠PBC=∠CAD=60°;进而证明△PBC为等边三角形,得到∠P=60°;结合∠CAF=∠PDC,问题即可解决.
解答: 解:△AFC∽△DCP;理由如下:
解:△AFC∽△DCP;理由如下:
∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴∠ACD=∠CAD=60°;AC=DC=
;
∴∠PBC=∠CAD=60°,而∠BP=BC,
∴△PBC为等边三角形,∠P=60°;
∵∠ACF=60°,∠CAF=∠PDC,
∴△AFC∽△DCP.
在△ABC与△DPC中,
∵
,
∴△ABC与△DPC(ASA),
PD=AB;
由圆及等边三角形的对称性知:
AF平分CD,
∴AB⊥CD;而AB为⊙O的直径,
∴∠ACB=90°;
由射影定理得:AC2=AF•AB,
∴AB=
=
,
∴PD=AB=
.
 解:△AFC∽△DCP;理由如下:
解:△AFC∽△DCP;理由如下:∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴∠ACD=∠CAD=60°;AC=DC=
| 3 |
∴∠PBC=∠CAD=60°,而∠BP=BC,
∴△PBC为等边三角形,∠P=60°;
∵∠ACF=60°,∠CAF=∠PDC,
∴△AFC∽△DCP.
在△ABC与△DPC中,
∵
|
∴△ABC与△DPC(ASA),
PD=AB;
由圆及等边三角形的对称性知:
AF平分CD,
∴AB⊥CD;而AB为⊙O的直径,
∴∠ACB=90°;
由射影定理得:AC2=AF•AB,
∴AB=
(
| ||
|
| 15 |
| 8 |
∴PD=AB=
| 15 |
| 8 |
点评:该题主要考查了等边三角形的判定、圆周角定理及其推论、相似三角形的判定及其性质等重要几何知识点的应用问题;解题的关键是深入观察探究、大胆猜测推理、科学解答论证.

练习册系列答案
相关题目
为了丰富人民的生活,泗阳县政府投资110000000元兴建了生态公园,110000000元用科学记数法表示应为( )
| A、1.169×109元 |
| B、1.1×108元 |
| C、11×108元 |
| D、0.11×109元 |
 如图所示,已知∠AOB=∠COD=90°,找出图中其他相等的角及图中互余的角.
如图所示,已知∠AOB=∠COD=90°,找出图中其他相等的角及图中互余的角.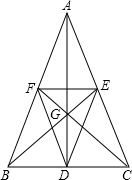 如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.
如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.