题目内容
4.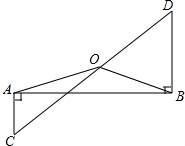 如图:AC⊥AB,DB⊥AB,OC=OD.求证:OA=OB.
如图:AC⊥AB,DB⊥AB,OC=OD.求证:OA=OB.
分析 延长AO交BD于E,通过△ACO≌△DOE,得到AO=OE,根据直角三角形斜边上的中线等于斜边的一半,可得答案AO=BO.
解答 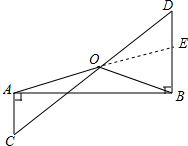 解:延长AO交BD于E,
解:延长AO交BD于E,
∵AC⊥AB,DB⊥AB,
∴AC∥BD,
∴∠C=∠D,
在△ACO与△DOE中,
$\left\{\begin{array}{l}{∠C=∠D}\\{∠AOC=∠DOE}\\{OC=OD}\end{array}\right.$,
∴△ACO≌△DOE,
∴AO=OE,
∵∠ABD=90°,
∴BO=$\frac{1}{2}$AE,
∴AO=BO.
点评 本题考查了全等三角形的性质,直角三角形的性质,平行线的判定,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
15.一元二次方程x2-3x-7=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 有一个实数根 |
12.A、B两地相距80千米,一辆大汽车从A地开出2小时后,又从A地开出另一辆小汽车,已知小汽车的速度是大汽车速度的3倍,结果小汽车比大汽车早40分钟到达B地,求两种汽车每小时各走多少千米.设大汽车的速度为xkm/h,则下面所列方程正确的是( )
| A. | $\frac{80}{x}$-$\frac{80}{3x}$=40 | B. | $\frac{80}{x}$-$\frac{80}{3x}$=2.4 | C. | $\frac{80}{x}$-2=$\frac{80}{3x}$+$\frac{2}{3}$ | D. | $\frac{80}{x}$+2=$\frac{80}{3x}$-$\frac{2}{3}$ |
14.已知三角形的两条边长分别为4cm和9cm,则其第三边长可能为( )
| A. | 4cm | B. | 5cm | C. | 6cm | D. | 13cm |
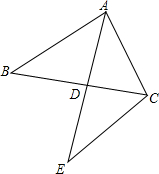 已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.
已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E. 如图所示,已知AB=AE,∠ABC=∠AED,BC=ED,F是CD的中点,AF与CD有什么位置关系?说明理由.
如图所示,已知AB=AE,∠ABC=∠AED,BC=ED,F是CD的中点,AF与CD有什么位置关系?说明理由.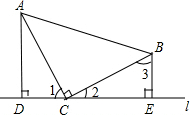 如图,在△ABC中,∠ACB=90°,CA=BC,直线l在△ABC的外部且过点C,AD⊥l,BE⊥l,垂足分别为点D、E.
如图,在△ABC中,∠ACB=90°,CA=BC,直线l在△ABC的外部且过点C,AD⊥l,BE⊥l,垂足分别为点D、E.