题目内容
11．
如图，在△ABC中，点D，E分别是AC，AB上的两点，且$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$，若△ADE的面积为1cm2，则四边形EBCD的面积为（ ）cm2．| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 由相似三角形的判定方法证明△ADE∽△ABC，由相似三角形的面积比等于相似比的平方求出△ABC的面积，即可得出四边形EBCD的面积．
解答 就：∵$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$，∠A=∠A，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{1}{2}$）2=$\frac{1}{4}$，
即$\frac{1}{{S}_{△ABC}}$=$\frac{1}{4}$，
解得：S△ABC=4，
∴四边形EBCD的面积=S△ABC-S△ADE=4-1=3（cm2）．
故选：B．
点评 本题考查了相似三角形的判定与性质；熟记相似三角形面积的比等于相似比的平方是解题的关键．
练习册系列答案
相关题目
16．
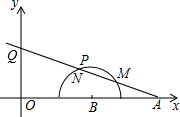如图，在平面直角坐标系xOy中，点A，B的坐标分别为（4，0），（2，0），现以B为圆心，1为半径在第一象限内画半圆，M，N是此半圆的三等分点，点P在$\widehat{MN}$上，射线AP交y轴于点Q，当点P从点M运动到点N时，点Q相应移动的路径长为（ ）
如图，在平面直角坐标系xOy中，点A，B的坐标分别为（4，0），（2，0），现以B为圆心，1为半径在第一象限内画半圆，M，N是此半圆的三等分点，点P在$\widehat{MN}$上，射线AP交y轴于点Q，当点P从点M运动到点N时，点Q相应移动的路径长为（ ）| A． | $\frac{2}{3}$$\sqrt{3}$ | B． | $\frac{8}{15}$$\sqrt{3}$ | C． | 2-$\frac{4}{5}$$\sqrt{3}$ | D． | 2$\sqrt{3}$-2 |
如图，在10×6的网格中，每个小正方形的边长都为1，每个小正方形的顶点称为格点，△AOB的顶点都在格点上，且O点是直角坐标系的原点．