题目内容
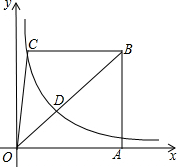 如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=| k |
| x |
考点:反比例函数综合题
专题:
分析:首先过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,由矩形与反比例函数的性质,可得S四边形ABDF=S△OBC=4,易证得△ODF∽△OBA,又由OD:DB=1:2,即可得S△ODF=
S四边形ABDF=
×4=
,则可求得答案.
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
解答: 解:过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,
解:过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,
∵梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,
∴四边形OABE是矩形,
∴S△OBE=S△OAB,
∵过点C的双曲线y=
交OB于点D,
∴S△OCE=S△ODF,
∴S四边形ABDF=S△OBC=4,
∵DF∥AB,
∴△ODF∽△OBA,
∵OD:DB=1:2,
∴OD:OB=1:3,
∴S△ODF:S△OAB=1:9,
∴S△ODF:S四边形ABDF=1:8,
∴S△ODF=
S四边形ABDF=
×4=
,
∴k=1.
故答案为:1.
 解:过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,
解:过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,∵梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,
∴四边形OABE是矩形,
∴S△OBE=S△OAB,
∵过点C的双曲线y=
| k |
| x |
∴S△OCE=S△ODF,
∴S四边形ABDF=S△OBC=4,
∵DF∥AB,
∴△ODF∽△OBA,
∵OD:DB=1:2,
∴OD:OB=1:3,
∴S△ODF:S△OAB=1:9,
∴S△ODF:S四边形ABDF=1:8,
∴S△ODF=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
∴k=1.
故答案为:1.
点评:此题属于反比例函数综合题,考查了反比例函数k的几何意义、矩形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
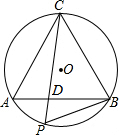 如图,等边△ABC内接于⊙O,点P是劣弧
如图,等边△ABC内接于⊙O,点P是劣弧
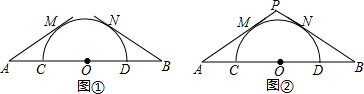
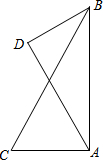 如图,一艘科学考察船由港口A出发沿正北方向航行,在航线的一侧有两个小岛C、D.考察船在A处时,测得小岛C在船的正西方,小岛D在船的北偏西30°方向.考察船向北航行了12千米到B处时,测得小岛C在船的南偏西30°方向,小岛D在船的南偏西60°方向.求小岛C、D之间的距离.
如图,一艘科学考察船由港口A出发沿正北方向航行,在航线的一侧有两个小岛C、D.考察船在A处时,测得小岛C在船的正西方,小岛D在船的北偏西30°方向.考察船向北航行了12千米到B处时,测得小岛C在船的南偏西30°方向,小岛D在船的南偏西60°方向.求小岛C、D之间的距离. 如图所示,数轴上在-2和-1之间的长度以小隔线分成八等分,A点在其中一隔,则A点表示的数是
如图所示,数轴上在-2和-1之间的长度以小隔线分成八等分,A点在其中一隔,则A点表示的数是