题目内容
15.计算:(1)2$\sqrt{\frac{1}{3}}$-$\sqrt{300}$
(2)$\frac{\sqrt{6}×\sqrt{3}}{\sqrt{2}}$-($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)
分析 (1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)先利用二次根式的乘除法则和平方差公式运算,然后合并即可.
解答 解:(1)原式=$\frac{2\sqrt{3}}{3}$-10$\sqrt{3}$
=-$\frac{28\sqrt{3}}{3}$;
(2)原式=$\sqrt{\frac{6×3}{2}}$-(3-2)
=3-1
=2.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
5.下列说法中,错误的是( )
| A. | 单项式-a2bc的系数是-1,次数是4 | |
| B. | 整式可分为单独一个数字、单独一个字母、单项式、多项式 | |
| C. | 多项式4a2-3b是二次二项式 | |
| D. | 4(3-x)2与-2(x-3)2可以看作是同类项 |
6.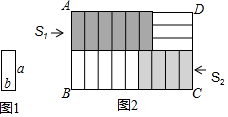 已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
 已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )| A. | 5b=2a | B. | 2b=a | C. | 3b=a | D. | 5b=3a |
3.为了了解2015年我市七年级学生期末考试的数学成绩,从中随机抽取了1000名学生的数学成绩进行分析,下列说法正确的是( )
| A. | 2015年我市七年级学生是总体 | |
| B. | 样本容量是1000 | |
| C. | 1000名七年级学生是总体的一个样本 | |
| D. | 每一名七年级学生是个体 |
20.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1,y2,y3的大小关系是
( )
( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
4.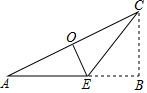 如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
 如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )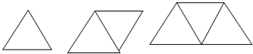 请你拿出火柴棒,现在我们来用火柴棒搭如图所示的三角形.
请你拿出火柴棒,现在我们来用火柴棒搭如图所示的三角形.