题目内容
4.关于x的一元二次方程x2-(2k-1)x+k2-2=0有两个不相等实数根α,β.(1)求k的取值范围;
(2)当(a-1)(β-1)=3,时,求α2+α-2β-1的值.
分析 (1)由于关于x的一元二次方程x2-(2k-1)x+k2-2=0有两个不相等的实数根α、β,那么其判别式应该是一个正数,由此即可求出k的取值范围;
(2)根据根与系数的关系可以得到α+β=2k-1,αβ=k2-2,(a-1)(β-1)=3,由此可以求出k的值,再把α2+α-2β-1变为-2(α+β),代入前面的值就可以求出结果.
解答 解:(1)∵方程x2-(2k-1)x+k2-2=0有两个不相等的实数根,
∴△>0即(2k-1)2-4×1×(k2-2)>0
解得k<$\frac{9}{4}$;
(2)由根与系数的关系得:α+β=2k-1,αβ=k2-2.
∵(a-1)(β-1)=αβ-(α+β)=3,
∴k2-2k-3=0
解得k=3或k=-1,
由(1)可知k=3不合题意,舍去.
∴k=-1,
原方程为x2+3x-1=0
∴α+β=-3,αβ=-1,α2=1-3α
∴α2+α-2β-1=1-3α+α-2β-1=-2(α+β)=6.
点评 此题考查根的判别式与根与系数的关系,首先利用一元二次方程的判别式求出k的取值范围,然后利用根与系数的关系求出k的值,接着把所求的代数式变形为两根之和与两根之积的形式,代入值就解决问题.

练习册系列答案
相关题目
15.将(-20)+(+3)-(-5)-(+7)改写成省略加号的和应是( )
| A. | -20+3-5+7 | B. | -20+3+5+7 | C. | -20+3+5-7 | D. | -20+3-5-7 |
9.成都市出租车的收费标准是:起步价9元,当路程超过2km时,每超过1km加收1.4元.若出租车行驶akm(a>2),则乘客应付费( )元.
| A. | 9+1.4a | B. | 9+1.4(a-2) | C. | 9-1.4a | D. | 9-1.4(a-2) |
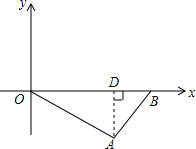 如图所示,已知在直角三角形OAB中,斜边OB在x轴正半轴上,直角顶点A在第四象限内,S△OAB=20,OA:AB=2:1,求A、B两点的坐标.
如图所示,已知在直角三角形OAB中,斜边OB在x轴正半轴上,直角顶点A在第四象限内,S△OAB=20,OA:AB=2:1,求A、B两点的坐标.