题目内容
14.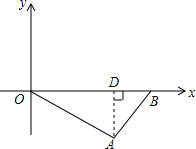 如图所示,已知在直角三角形OAB中,斜边OB在x轴正半轴上,直角顶点A在第四象限内,S△OAB=20,OA:AB=2:1,求A、B两点的坐标.
如图所示,已知在直角三角形OAB中,斜边OB在x轴正半轴上,直角顶点A在第四象限内,S△OAB=20,OA:AB=2:1,求A、B两点的坐标.
分析 设AB为x,则OA为2x,根据勾股定理和三角形的面积公式求出AD、OD和OB的长,确定A、B两点的坐标.
解答 解:设AB为x,则OA为2x,
由勾股定理得,OB=$\sqrt{5}$x,
$\frac{1}{2}$×OA×OB=$\frac{1}{2}$×OB×AD,
∴AD=$\frac{2\sqrt{5}}{5}$x,
∵S△OAB=20,
∴$\frac{1}{2}$×x×2x=20,
解得x=2$\sqrt{5}$,
则OA=4$\sqrt{5}$,AD=4,OB=10,
由勾股定理得,OD=$\sqrt{O{A}^{2}-A{D}^{2}}$=8,
∴A点的坐标为(8,-4
B点的坐标(10,0).
点评 本题考查的是勾股定理和坐标与图形的性质,运用勾股定理求出有关的边的长度是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列方程中,是一元二次方程的是( )
| A. | x-y2=1 | B. | 2x+1=0 | C. | $\frac{1}{x^2}-1=0$ | D. | $\frac{x^2}{2}-\frac{x-1}{3}=0$ |
6.已知关于x的方程x2-3x+c=0有一根是x=1,那么这个方程的另一个根是( )
| A. | x=2 | B. | x=-2 | C. | x=-4 | D. | 4 |
4.如果两个相似三角形对应边中线之比是1:4,那么它们的对应高之比是( )
| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连接AF,BF,则∠ABF的度数是30°.
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连接AF,BF,则∠ABF的度数是30°.