题目内容
1. 如图,将两张长为6cm,宽为3cm的矩形纸条交叉,使重叠部分是一个菱形,那么菱形周长的最大值是15.
如图,将两张长为6cm,宽为3cm的矩形纸条交叉,使重叠部分是一个菱形,那么菱形周长的最大值是15.
分析 根据重叠部分构成的菱形的周长最大,边长也最大,此时设菱形的边长为x,然后表示出BC,再利用勾股定理列式进行计算即可求出x的值,然后根据菱形的周长公式列式进行计算即可得解.
解答  解:如图所示时,重叠部分构成的菱形的周长最大,
解:如图所示时,重叠部分构成的菱形的周长最大,
设AB=x,
∵矩形纸条的长为6cm,宽为3cm,
∴BC=(6-x)cm,
在Rt△ABC中,AB2=AC2+BC2,
即x2=32+(6-x)2,
整理得,12x=45,
解得x=$\frac{15}{4}$,
故菱形周长的最大值4×$\frac{15}{4}$=15cm.
故答案为:15cm.
点评 本题考查了菱形的性质,利用菱形的面积确定出菱形的边长最大时的情况是解题的关键,还利用了勾股定理.

练习册系列答案
相关题目
11.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{6}$ | C. | $\sqrt{9}$ | D. | $\sqrt{18}$ |
9.如果2x3-m=y是二元一次方程,则m是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
6.要组织一次篮球邀请赛,参赛的每两个队之间都要比赛一场,据场地和时间等条件的限制,赛程计划安排7天,每天安排4场比赛,刚好完成所有比赛.设比赛组织者邀请x个队参赛,则根据题意所列方程正确的是( )
| A. | $\frac{1}{2}$x(x+1)=28 | B. | $\frac{1}{2}$x(x-1)=28 | C. | x(x+1)=28 | D. | x(x-1)=28 |
13.下列各式从左边到右边的变形中,是因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2-4+2x=(x+2)(x-2)+2x | ||
| C. | 2a(b-c)=2ab-2ac | D. | m2-n2=(m+n)(m-n) |
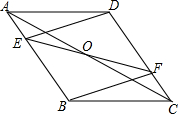 如图所示,O为?ABCD对角线AC的中点,EF经过点O交AB于E,交CD于点F,连接DE、BF.求证:四边形EBFD为平行四边形.
如图所示,O为?ABCD对角线AC的中点,EF经过点O交AB于E,交CD于点F,连接DE、BF.求证:四边形EBFD为平行四边形.