题目内容
7. 如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,求证:MF>DC.
如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,求证:MF>DC.
分析 根据折叠的性质得∠EAB=∠EAN,AN=AB=6,由于AB∥CD,则∠FAB=∠F,所以∠FAM=∠F,得到MA=MF,在Rt△ADM中,得出答案即可.
解答 证明:∵△ABE沿直线AE翻折,点B落在点N处,
∴∠EAB=∠EAN,
∵四边形ABCD为正方形,
∴AB∥CD,
∴∠FAB=∠F,
∴∠FAM=∠F,
∴MA=MF,
在Rt△ADM中,
∵AM>AD,
∴MF>DC.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
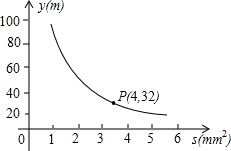 兰州是拉面的故乡,在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示,若工人师傅将面团拉成160根,每根长0.5m时为成品,则此时拉面粗1.6mm2.
兰州是拉面的故乡,在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示,若工人师傅将面团拉成160根,每根长0.5m时为成品,则此时拉面粗1.6mm2.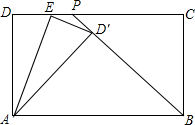 如图,在矩形ABCD中,BP是角平分线,E是CD上一点,将△ADE沿AE翻折,使D落在BP上,AD=5,CD=7,求DE的长度.
如图,在矩形ABCD中,BP是角平分线,E是CD上一点,将△ADE沿AE翻折,使D落在BP上,AD=5,CD=7,求DE的长度.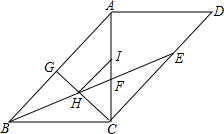 如图,平行四边形ABCD中,对角线AC⊥BC,BE平分∠ABC,交CD于点E,且与AC交于点F.过点C作CG1AB于点G,CG与BE交于点H,点I在线段AC上,且HI∥AB.求证:
如图,平行四边形ABCD中,对角线AC⊥BC,BE平分∠ABC,交CD于点E,且与AC交于点F.过点C作CG1AB于点G,CG与BE交于点H,点I在线段AC上,且HI∥AB.求证: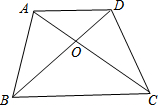 梯形ABCD中,AD∥BC,对角线AC、BD交于点O,若AD=3,BC=5,则S△AOD:S△DOC=3:5.
梯形ABCD中,AD∥BC,对角线AC、BD交于点O,若AD=3,BC=5,则S△AOD:S△DOC=3:5.