题目内容
17.如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足$(a+4{)^2}+\sqrt{b-4}=0$,过C作CB⊥x轴于B.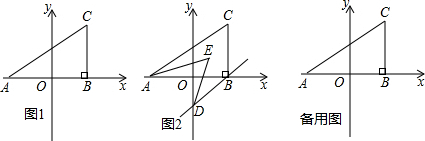
(1)求△ABC的面积.
(2)在y轴上是否存在点P,使得△ABC和△ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
分析 (1)根据非负数的性质易得a=-4,b=4,然后根据三角形面积公式计算;
(2)分类讨论:设P(0,t),当P在y轴正半轴上时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC-S△ANP-S△CMP=8可得到关于t的方程,再解方程求出t;
(3)过E作EF∥AC,根据平行线性质得BD∥AC∥EF,且∠3=$\frac{1}{2}$∠CAB=∠1,∠4=$\frac{1}{2}$∠ODB=∠2,所以∠AED=∠1+∠2=$\frac{1}{2}$(∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90° 代入计算即可.
解答 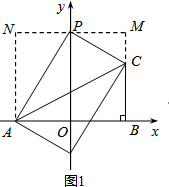 解:(1)∵(a+4)2+$\sqrt{b-4}$=0,
解:(1)∵(a+4)2+$\sqrt{b-4}$=0,
∴a+4=0,b-4=0,
∴a=-4,b=4,
∵CB⊥AB
∴A(-4,0),B(4,0),C(4,2),
∴△ABC的面积=$\frac{1}{2}$×2×8=8;
(2)①当P在y轴正半轴上时,如图1,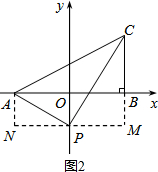
设P(0,t),
过P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=8,
∴$\frac{1}{2}$×8×(t+t-2)-$\frac{1}{2}$×4t-$\frac{1}{2}$×4×(t-2)=8,
解得:t=3,
②当P在y轴负半轴上时,如图2,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=8
∴$\frac{1}{2}$×8(-t+2-t)+$\frac{1}{2}$×4t-$\frac{1}{2}$×4(2-t)=8,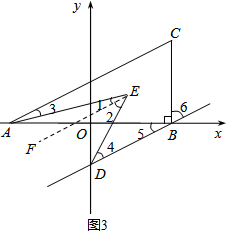
解得:t=-1,
∴P(0,-1)或(0,3).
(3)∵CB∥y轴,BD∥AC,
∴∠CAB=∠5,∠ODB=∠6,∠CAB+∠ODB=∠5+∠6=90°,
过E作EF∥AC,如图3,
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=$\frac{1}{2}$∠CAB=∠1,∠4=$\frac{1}{2}$∠ODB=∠2,
∴∠AED=∠1+∠2=$\frac{1}{2}$(∠CAB+∠ODB)=45°.
点评 本题考查了平行线的判定与性质:两直线平行,内错角相等.也考查了非负数的性质、坐标与图形性质以及三角形面积公式.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案| A. | 1,2,4 | B. | 4,9,6 | C. | 5,5,11 | D. | 3,5,8 |
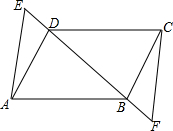 如图,在四边形ABCD中,点E、F在直线BD上,AE=CF,AD=CB,BE=DF.
如图,在四边形ABCD中,点E、F在直线BD上,AE=CF,AD=CB,BE=DF.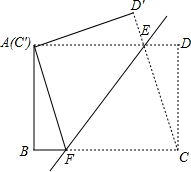 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.①AF=CD′;②△CEF是等腰三角形;③四边形AFCE为菱形;④设AE=a,ED=b,DC=c,则a、b、c三者之间的数量关系为a2=b2+c2,其中正确的结论是②③④(将所有正确结论的序号都填在横线上)
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.①AF=CD′;②△CEF是等腰三角形;③四边形AFCE为菱形;④设AE=a,ED=b,DC=c,则a、b、c三者之间的数量关系为a2=b2+c2,其中正确的结论是②③④(将所有正确结论的序号都填在横线上)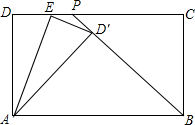 如图,在矩形ABCD中,BP是角平分线,E是CD上一点,将△ADE沿AE翻折,使D落在BP上,AD=5,CD=7,求DE的长度.
如图,在矩形ABCD中,BP是角平分线,E是CD上一点,将△ADE沿AE翻折,使D落在BP上,AD=5,CD=7,求DE的长度.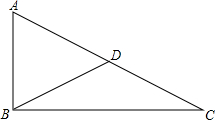 已知在△ABC中,∠A=3∠C,∠ADB=45°,D为AC的中点,求证:∠ABC=90°.
已知在△ABC中,∠A=3∠C,∠ADB=45°,D为AC的中点,求证:∠ABC=90°.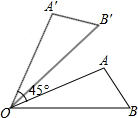 如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.
如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.