题目内容
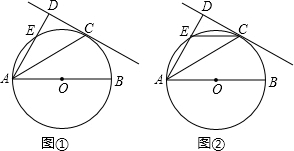 已知AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于点E,∠CAB=30°.
已知AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于点E,∠CAB=30°.(I)如图①,求∠DAC的大小;
(II)如图②,若⊙O的直径为8,求DE的长.
考点:切线的性质,等边三角形的判定与性质
专题:
分析:(Ⅰ)连接OC,由切线的性质可知OC⊥DC因为AD⊥DC,所以OC∥AD,由平行线的性质可得:∠DAC=∠CAB=30°;
(Ⅱ)连接OE,OC,首先可证明△AOE是等边三角形,所以AE=AO=4,根据DE=AD-AE计算即可.
(Ⅱ)连接OE,OC,首先可证明△AOE是等边三角形,所以AE=AO=4,根据DE=AD-AE计算即可.
解答: 解:(Ⅰ)连接OC,
解:(Ⅰ)连接OC,
∵DC是圆的切线,
∴OC⊥DC,
∵AD⊥DC,
∴OC∥AD,
∴∠DAC=∠CAB=30°;
(Ⅱ)连接OE,OC,
∵∠EAO=∠DAC+∠CAB=60°,OE=OA,
∴△AOE是等边三角形,
∴AE=AO=
AB=4,
∵AB=8,∠CAB=30°,
∴AC=8×cos30°=4
,
∴AD=AC•cos30°=6,
∴DE=AD-AE=6-4=2.
 解:(Ⅰ)连接OC,
解:(Ⅰ)连接OC,∵DC是圆的切线,
∴OC⊥DC,
∵AD⊥DC,
∴OC∥AD,
∴∠DAC=∠CAB=30°;
(Ⅱ)连接OE,OC,
∵∠EAO=∠DAC+∠CAB=60°,OE=OA,
∴△AOE是等边三角形,
∴AE=AO=
| 1 |
| 2 |
∵AB=8,∠CAB=30°,
∴AC=8×cos30°=4
| 3 |
∴AD=AC•cos30°=6,
∴DE=AD-AE=6-4=2.
点评:本题考查了切线的性质、平行线的判定和性质、等边三角形的判定和性质以及特殊角的锐角三角形函数值,题目的综合性较强,难度中等.

练习册系列答案
相关题目
若一个数的相反数是2,则这个数是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图,已知E为直线AD上一点,∠1=∠2,∠B=∠C,请写出图中一组相等的线段
如图,已知E为直线AD上一点,∠1=∠2,∠B=∠C,请写出图中一组相等的线段 如图,已知四边形ABCD中,∠A=∠B=∠DEC,且点E为AB边中点,则图中有
如图,已知四边形ABCD中,∠A=∠B=∠DEC,且点E为AB边中点,则图中有