题目内容
在Rt△ABC中，∠C=90°，cosB=
，则a：b= ．
| 2 |
| 3 |
考点：解直角三角形
专题：
分析：根据∠B的余弦得到a边与c边的关系，然后用勾股定理求出b边，可以得到它们的比值．
解答：解：由cosB=
，可以设a=2x，c=3x，
用勾股定理有：b=
=
=
x．
∴a：b=2x：
x=2：
．
故答案为2：
．
| 2 |
| 3 |
用勾股定理有：b=
| c2-a2 |
| (3x)2-(2x)2 |
| 5 |
∴a：b=2x：
| 5 |
| 5 |
故答案为2：
| 5 |
点评：本题考查的是锐角三角函数的定义，根据锐角三角函数的定义可以得到a与c的关系，然后用勾股定理计算出b边，就可以确定a：b的值．
练习册系列答案
相关题目
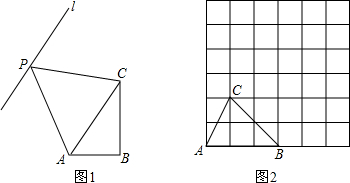
如图，在正方形网格中，点O、A、B均在格点上，则∠AOB的正弦值是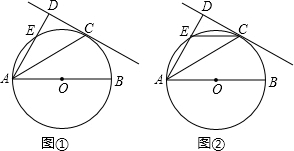
已知AB为⊙O的直径，C为⊙O上一点，AD与过C点的切线垂直，垂足为D，AD交⊙O于点E，∠CAB=30°．
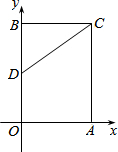在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，求点E、F的坐标分别为下列计算不正确的是（ ）
| A、π0=1 | ||
B、2014-1=
| ||
| C、（-1）2014=1 | ||
D、
|
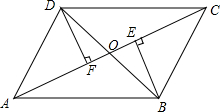如图，四边形ABCD的对角线AC、BD交于点O，BE⊥AC于E，DF⊥AC于F，点O既是AC的中点，又是EF的中点．