题目内容
3.对点(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1[Pn-1(x,y)](n为大于1的整数).
如P1(1,2)=(3,-1),P2(1,2)=P1[P1(1,2)]=P1(3,-1)=(2,4),P3(1,2)=P1[P2(1,2)]=P1(2,4)=(6,-2).
(1)P1(1,-1)=(0,2)
P2(1,-1)=P1[P1(1,-1)]=P1(0,2)=(2,-2)
P3(1,-1)=P1[P2(1,-1)]=P1(2,-2)=(0,4)
P4(1,-1)=P1[P3(1,-1)]=P1(0,4)=(4,-4)
(2)根据(1)的规律求P5(1,-1),P6(1,-1),P2013(1,-1).
分析 根据所给的已知条件,找出题目中的变化规律,得出当n分别为奇数和偶数时的坐标,即可解决问题.
解答 解:(1)根据题意得:
P1(1,-1)=(0,2),
P2(1,-1)=P1[P1(1,-1)]=P1(0,2)=(2,-2)
P3(1,-1)=P1[P2(1,-1)]=P1(2,-2)=(0,4),
P4(1,-1)=P1[P3(1,-1)]=P1(0,4)=(4,-4)
故答案为:0,2;0,2;2,-2;2,-2;0,4;0,4;4,-4;
(2)根据(1)的规律可知;
P5(1,-1)=P1[P4(1,-1)]=P1(4,-4)=(0,8),
P6(1,-1)=P1[P5(1,-1)]=P1(0,8)=(8,-8),
…
当n为奇数时,Pn(1,-1)=)=(0,${2}^{\frac{n+1}{2}}$),
当n为偶数时,Pn(1,-1)=(${2}^{\frac{n}{2}}$,-${2}^{\frac{n}{2}}$),
∴P2013(1,-1)=(0,21007).
点评 本题考查了点的坐标,解题的关键是找出数字的变化,得出当n为偶数时的规律,并应用此规律解题.

练习册系列答案
相关题目
14.矩形的两邻边长的差为2,对角线长为4,则矩形的面积为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,求阴影部分的面积.
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,求阴影部分的面积.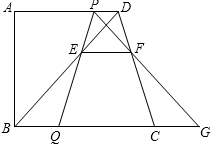 如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13,AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.
如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13,AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.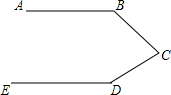 如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件合格.(填“合格”或“不合格”)
如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件合格.(填“合格”或“不合格”)