题目内容
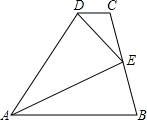 如图,在四边形ABCD中,AB∥CD,点E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
如图,在四边形ABCD中,AB∥CD,点E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:先过点E作EH⊥AB于点H,反向延长EH交DC的延长线于点G,过点E作EF⊥AD于点F,由平行线的性质可知EG⊥AC,由于E是BC的中点,可得出Rt△CGE≌Rt△BHE,故GE=EH,再根据角平分线的性质可知EF=GE,故EF=EH,进而可得出结论.
解答: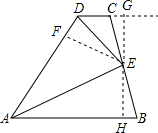 解:过点E作EH⊥AB于点H,反向延长EH交DC的延长线于点G,过点E作EF⊥AD于点F,
解:过点E作EH⊥AB于点H,反向延长EH交DC的延长线于点G,过点E作EF⊥AD于点F,
∵AB∥CD,EH⊥AB,
∴EG⊥DC,
∵点E是BC的中点,
∴CE=BE,
在△CGE与△BHE中,
,
∴△CGE≌△BHE,
∴GE=EH,
∵DE平分∠ADC,
∴GE=EF,
∴GE=EH,
∴EF=EH,
∴AE是∠DAB的平分线.
 解:过点E作EH⊥AB于点H,反向延长EH交DC的延长线于点G,过点E作EF⊥AD于点F,
解:过点E作EH⊥AB于点H,反向延长EH交DC的延长线于点G,过点E作EF⊥AD于点F,∵AB∥CD,EH⊥AB,
∴EG⊥DC,
∵点E是BC的中点,
∴CE=BE,
在△CGE与△BHE中,
|
∴△CGE≌△BHE,
∴GE=EH,
∵DE平分∠ADC,
∴GE=EF,
∴GE=EH,
∴EF=EH,
∴AE是∠DAB的平分线.
点评:本题考查的是角平分线的性质及全等三角形的判定与性质,根据题意做出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
甲、乙、丙三人用擂台赛形式进行训练.每局两人单打比赛,另一人当裁判.每一局输者当下一局的裁判,而原来的裁判与赢者比赛.一天训练结束时,统计甲共打12局,乙共打21局,而丙共当裁判8局.那么整个比赛中第10局的输者( )
| A、必是甲 | B、必是乙 |
| C、必是丙 | D、不能确定 |
 如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=
如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=
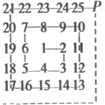 友谊公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果P处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处(编号2在第1个拐角处)的竹子的编号应为( )
友谊公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果P处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处(编号2在第1个拐角处)的竹子的编号应为( )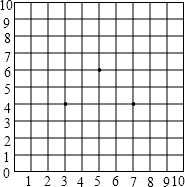 在图的方格棋盘中放入3枚棋子,位置分别是(3,4),(7,4),(5,6).这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个正方形?如果能,请说出放在什么位置.
在图的方格棋盘中放入3枚棋子,位置分别是(3,4),(7,4),(5,6).这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个正方形?如果能,请说出放在什么位置.