题目内容
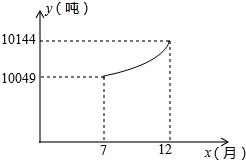 企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年下半年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.7至12月,该企业自身处理的污水量y(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y=ax2+c(a≠0),其图象如图所示.污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年下半年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.7至12月,该企业自身处理的污水量y(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y=ax2+c(a≠0),其图象如图所示.污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.(1)请观察题中图象,请你求出y与x之间的函数关系式;
(2)请你求出该企业去年下半年哪个月用于污水处理的费用W(元)最多,并求出这个最多费用;
(3)今年以来,由于自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加(a-30)%,为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行50%的补助.若该企业每月的污水处理费用为18000元,请计算出a的整数值.
(注:结果保留整数.参考数据:
| 231 |
| 419 |
| 809 |
考点:二次函数的应用
专题:
分析:(1)利用函数图象得出:图象过(7,10049),(12,10144)点,求出解析式即可;
(2)利用当7≤x≤12时,求出处理污水的费用,即可得出答案;
(3)利用今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加(a一30)%,得出等式12000(1+a%)×1.5×[1+(a-30)%]×(1-50%)=18000,进而求出即可.
(2)利用当7≤x≤12时,求出处理污水的费用,即可得出答案;
(3)利用今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加(a一30)%,得出等式12000(1+a%)×1.5×[1+(a-30)%]×(1-50%)=18000,进而求出即可.
解答:解:(1)根据图象可以得出:图象过(7,10049),(12,10144)点,
代入y2=ax2+c(a≠0)得:
,
解得:
,
故y=x2+10000(7≤x≤12,且x取整数);
(2)当7≤x≤12时,且x取整数时,
W=2×(12000-y2)+1.5y2=2×(12000-x2-10000)+1.5(x2+10000),
=-
x2+19000,
∵a=-
<0,x=-
=0,
当7≤x≤12时,W随x的增大而减小,
∴当x=7时,W最大=18975.5(元),
∵22000>18975.5,
∴去年5月用于污水处理的费用最多,最多费用是22000元;
(3)由题意得:12000(1+a%)×1.5×[1+(a-30)%]×(1-50%)=18000,
设t=a%,整理得:10t2+17t-13=0,
解得:t=
,
∵
≈28.4,
∴t1≈0.57,t2≈-2.27(舍去),
∴a≈57,
答:a的值是57.
代入y2=ax2+c(a≠0)得:
|
解得:
|
故y=x2+10000(7≤x≤12,且x取整数);
(2)当7≤x≤12时,且x取整数时,
W=2×(12000-y2)+1.5y2=2×(12000-x2-10000)+1.5(x2+10000),
=-
| 1 |
| 2 |
∵a=-
| 1 |
| 2 |
| b |
| 2a |
当7≤x≤12时,W随x的增大而减小,
∴当x=7时,W最大=18975.5(元),
∵22000>18975.5,
∴去年5月用于污水处理的费用最多,最多费用是22000元;
(3)由题意得:12000(1+a%)×1.5×[1+(a-30)%]×(1-50%)=18000,
设t=a%,整理得:10t2+17t-13=0,
解得:t=
-17±
| ||
| 20 |
∵
| 809 |
∴t1≈0.57,t2≈-2.27(舍去),
∴a≈57,
答:a的值是57.
点评:此题主要考查了二次函数的应用和根据实际问题列二次函数关系式、求二次函数最值等知识.此题阅读量较大,得出正确关于a%的等式方程是解题关键.

练习册系列答案
相关题目
已知一个多项式(m+1)x3y|m|+xy2+85是个四次三项式,那么m=( )
| A、1 | B、-1 | C、±1 | D、0 |
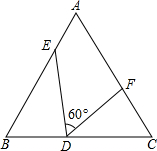 如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发,设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程始终保持∠EDF=60°.
如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发,设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程始终保持∠EDF=60°.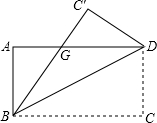 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.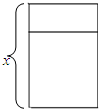 某校在新建学生宿舍时需如图所示的铝合金窗框(别忘了中间还用了一根),它共用了长8米的铝合金,设长方形窗框的一边长为x米(如图).
某校在新建学生宿舍时需如图所示的铝合金窗框(别忘了中间还用了一根),它共用了长8米的铝合金,设长方形窗框的一边长为x米(如图). 如图,在△ABC中,CA=CB,O为外心,I为内心,D为BC上的点,且BI⊥DO.
如图,在△ABC中,CA=CB,O为外心,I为内心,D为BC上的点,且BI⊥DO.