题目内容
已知一个多项式（m+1）x3y|m|+xy2+85是个四次三项式，那么m=（ ）
| A、1 | B、-1 | C、±1 | D、0 |
考点：多项式
专题：
分析：多项式（m+1）x3y|m|+xy2+85是个四次三项式，所以m+1≠0，3+|m|=4，据此确定m的值即可．
解答：解：∵多项式（m+1）x3y|m|+xy2+85是个四次三项式，
∴m+1≠0，3+|m|=4，
解得：m=1，
故选：A
∴m+1≠0，3+|m|=4，
解得：m=1，
故选：A
点评：本题考查了多项式的知识，属于基础题，本题容易忽略m+1≠0这一条件．
练习册系列答案
相关题目
在长方形ABCD中，BD是对角线，将△ABD沿直线BD折叠，点A落在点E处，BE与CD交于点F，则△DFB是分式
中的x，y都扩大6倍，则该分式的值（ ）
| xy |
| 2x+3y |
| A、不变 | B、扩大6倍 |
| C、缩小6倍 | D、扩大36倍 |
在梯形ABCD中，AD∥BC，那么∠A：∠B：∠C：∠D可能为（ ）
| A、3：4：5：2 |
| B、2：3：4：5 |
| C、5：3：4：2 |
| D、5：4：3：2 |
若z2-kz-15=（z+a）（z+b），则a+b的值不可能为（ ）
| A、14 | B、16 | C、2 | D、-14 |
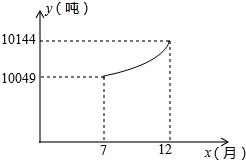企业的污水处理有两种方式，一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理．某企业去年下半年每月的污水量均为12000吨，由于污水厂处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同时进行．7至12月，该企业自身处理的污水量y（吨）与月份x（7≤x≤12，且x取整数）之间满足二次函数关系式为y=ax2+c（a≠0），其图象如图所示．污水厂处理每吨污水的费用均为2元，该企业自身处理每吨污水的费用均为1.5元．