题目内容
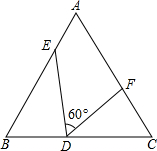 如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发,设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程始终保持∠EDF=60°.
如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发,设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程始终保持∠EDF=60°.(1)求证:∠EDB=∠DFC;
(2)当t=3秒时,求BE+CF的值;
(3)是否存在这样的t值,使得CF=
| 9 |
| 4 |
考点:等边三角形的性质
专题:动点型
分析:(1)利用∠CDF+∠EDB=120°和∠CDF+∠DFC=120°求证即可.
(2)利用△EBD∽△DFC得出
=
,求出CF,即可求出BE+CF的值;
(3)利用△EBD∽△DFC得出
=
=
,求出CD,BD及BE,利用E点由B点开始以2cm/秒的速度向A点运动,得出时间t.
(2)利用△EBD∽△DFC得出
| BE |
| BD |
| CD |
| CF |
(3)利用△EBD∽△DFC得出
| BE |
| BD |
| CD |
| CF |
| 1 |
| 2 |
解答:证明:(1)∵∠EDF=60°,
∴∠CDF+∠EDB=120°,
∵△ABC是等边三角形,
∴∠C=60°,
∴∠CDF+∠DFC=120°,
∴∠EDB=∠DFC;
(2)∵D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,
∴t=3秒,BE=6,BD=3,
∴CD=BC-BD=9-3=6,
∵△EBD∽△DFC,
∴
=
,即
=
,
∴CF=3,
∴BE+CF=6+3=9.
(3)存在,理由如下.
∵△EBD∽△DFC,
∴
=
=
,
∵CF=
cm,
∴CD=
,
∴BD=9-
=
,
∴BE=9,即t=
,
∴当t=
时,使得CF=
cm.
∴∠CDF+∠EDB=120°,
∵△ABC是等边三角形,
∴∠C=60°,
∴∠CDF+∠DFC=120°,
∴∠EDB=∠DFC;
(2)∵D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,
∴t=3秒,BE=6,BD=3,
∴CD=BC-BD=9-3=6,
∵△EBD∽△DFC,
∴
| BE |
| BD |
| CD |
| CF |
| 6 |
| 3 |
| 6 |
| CF |
∴CF=3,
∴BE+CF=6+3=9.
(3)存在,理由如下.
∵△EBD∽△DFC,
∴
| BE |
| BD |
| CD |
| CF |
| 1 |
| 2 |
∵CF=
| 9 |
| 4 |
∴CD=
| 9 |
| 2 |
∴BD=9-
| 9 |
| 2 |
| 9 |
| 2 |
∴BE=9,即t=
| 9 |
| 2 |
∴当t=
| 9 |
| 2 |
| 9 |
| 4 |
点评:本题主要考查了等边三角形的性质及相似三角形,解题的关键是明确△EBD∽△DFC利用对应边的比求解.

练习册系列答案
相关题目
分式
中的x,y都扩大6倍,则该分式的值( )
| xy |
| 2x+3y |
| A、不变 | B、扩大6倍 |
| C、缩小6倍 | D、扩大36倍 |
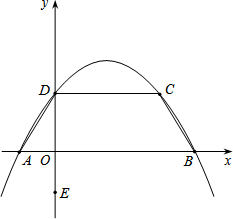 如图,抛物线y=-
如图,抛物线y=-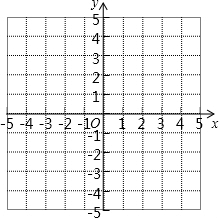 设一直角三角形的面积为8cm2,两直角边长分别为xcm和ycm.
设一直角三角形的面积为8cm2,两直角边长分别为xcm和ycm.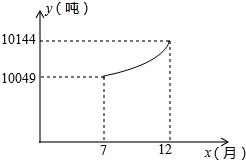 企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年下半年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.7至12月,该企业自身处理的污水量y(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y=ax2+c(a≠0),其图象如图所示.污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年下半年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.7至12月,该企业自身处理的污水量y(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y=ax2+c(a≠0),其图象如图所示.污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.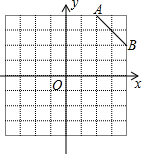 如图在8×8的正方形网格中建立直角坐标系,已 知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形,画出图形,并解答下列问题:
如图在8×8的正方形网格中建立直角坐标系,已 知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形,画出图形,并解答下列问题: