题目内容

已知样本x1，x2，x3，x4，x5平均数是5，方差是2，则x1-3，x2-3，x3-3，x4-3，x5-3的平均数为
 
；方差为
 
．
考点：方差,算术平均数
专题：
分析：根据平均数的变化规律可得出数据x1-3，x2-3，x3-3，x4-3，x5-3的平均数是5-3；先根据数据x1，x2，x3，x4，x5的方差为2，求出数据x1-3，x2-3，x3-3，x4-3，x5-3的方差是2．
解答：解：∵数据x1，x2，x3，x4，x5的平均数是5，
∴数据x1-3，x2-3，x3-3，x4-3，x5-3的平均数是5-3=2；
∵数据x1，x2，x3，x4，x5的方差为2，
∴数据x1-3，x2-3，x3-3，x4-3，x5-3的方差是2；
故答案为：2，2．
点评：此题考查了平均数和方差，一般地设n个数据，x1，x2，…xn的平均数为
.
x
，则方差S2=
1
n
[（x1-
.
x
）2+（x2-
.
x
）2+…+（xn-
.
x
）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
练习册系列答案
相关题目
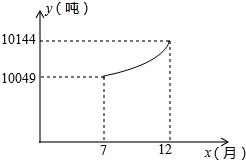企业的污水处理有两种方式，一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理．某企业去年下半年每月的污水量均为12000吨，由于污水厂处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同时进行．7至12月，该企业自身处理的污水量y（吨）与月份x（7≤x≤12，且x取整数）之间满足二次函数关系式为y=ax2+c（a≠0），其图象如图所示．污水厂处理每吨污水的费用均为2元，该企业自身处理每吨污水的费用均为1.5元．
（1）请观察题中图象，请你求出y与x之间的函数关系式；
（2）请你求出该企业去年下半年哪个月用于污水处理的费用W（元）最多，并求出这个最多费用；
（3）今年以来，由于自建污水处理设备的全面运行，该企业决定扩大产能并将所有污水全部自身处理，估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%，同时每吨污水处理的费用将在去年12月份的基础上增加（a-30）%，为鼓励节能降耗，减轻企业负担，财政对企业处理污水的费用进行50%的补助．若该企业每月的污水处理费用为18000元，请计算出a的整数值．
（注：结果保留整数．参考数据：
231
≈15.2，
419
≈20.5，
809
≈28.4）
操作与思考探索性问题：
已知点A，B在数轴上的位置所表示的数分别用a、b表示．利用数形结合思想回答下列问题：
（1）填写下表：
数第1组第2组第3组第4组第5组第6组…
a5-56-6-10-2.5…
b30-4-42-2.5…
A，B两点的距离20…
（2）通过对上表中具体数据的研究和归纳，你发现数轴上表示x和-2两点之间的距离表示为
 
．
（3）若x表示一个有理数，则|x-1|+|x+3|的最小值是
 
．
使代数式
2+x
有意义的x的取值范围是
 
．
在数轴上与-1相距3个单位长度的点表示的有理数是
 
．
化简：
2
•
3
=
 
．
如果3x2ym与-2xn-1y3是同类项，那么m+n=
 
．
一个直角三角形的两条边分别是3和2，则第三边的长度为
 
．
某班有60名学生，班长把全班学生对周末出游地的意向绘制成了扇形统计图，其中“想去重庆金佛山滑雪的学生数”的扇形圆心角是60°，则下列说法正确的是（　　）
A、想去重庆金佛山滑雪的学生有12人
B、想去重庆金佛山滑雪的学生肯定最多
C、想去重庆金佛山滑雪的学生占全班学生的
1
6
D、想去重庆金佛山滑雪的学生占全班学生的60%

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网