题目内容
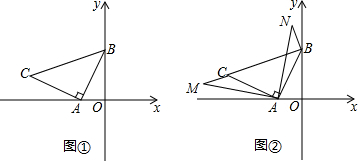
已知A(-1,0),B(0,2),AC⊥AB且AC=AB.
(1)求C点的坐标;
(2)如图②点M在BC的延长线上,且AM=AN,AM⊥AN,问CM与BN存在怎样的关系,并证明.
(1)求C点的坐标;
(2)如图②点M在BC的延长线上,且AM=AN,AM⊥AN,问CM与BN存在怎样的关系,并证明.

考点:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形
专题:
分析:(1)作CD⊥OA延长线于点D,易证∠CAD=∠ABO,即可证明△CDA≌△AOB,即可解题;
(2)易证∠MAC=∠NAB,即可证明△MAC≌△NAB,可得CM=BN,∠M=∠N,可证CM⊥BN,即可解题.
(2)易证∠MAC=∠NAB,即可证明△MAC≌△NAB,可得CM=BN,∠M=∠N,可证CM⊥BN,即可解题.
解答:解:(1)作CD⊥OA延长线于点D,
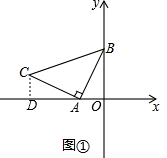
∵∠CAD+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠CAD=∠ABO,
在△CDA和△AOB中,
,
∴△CDA≌△AOB(AAS),
∴CD=AO,AD=BO,
∴点C坐标为(-3,1);
(2)如图②,
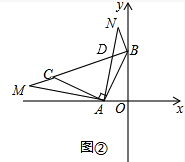
∵∠MAC+∠CAN=90°,∠CAN+∠NAB=90°,
∴∠MAC=∠NAB,
在△MAC和△NAB中,
,
∴△MAC≌△NAB(SAS),
∴CM=BN,∠M=∠N,
∵∠M+ADM=90°,∠ADM=∠BDN,
∴∠BDN+∠N=90°,
∴CM⊥BN,
∴CM与BN的关系为垂直且相等.

∵∠CAD+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠CAD=∠ABO,
在△CDA和△AOB中,
|
∴△CDA≌△AOB(AAS),
∴CD=AO,AD=BO,
∴点C坐标为(-3,1);
(2)如图②,

∵∠MAC+∠CAN=90°,∠CAN+∠NAB=90°,
∴∠MAC=∠NAB,
在△MAC和△NAB中,
|
∴△MAC≌△NAB(SAS),
∴CM=BN,∠M=∠N,
∵∠M+ADM=90°,∠ADM=∠BDN,
∴∠BDN+∠N=90°,
∴CM⊥BN,
∴CM与BN的关系为垂直且相等.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△CDA≌△AOB和△MAC≌△NAB是解题的关键.

练习册系列答案
相关题目
下列方程中,关于x的一元二次方程是( )
| A、3(x+1)2=(2x+1) | ||
B、x+
| ||
| C、ax2+bx+c=0 | ||
| D、x2+2x=x2-1 |
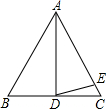 如图,在△ABC中,AB=AC,BD=CD,∠BAD=40°,且AD=AE,则∠EDC等于
如图,在△ABC中,AB=AC,BD=CD,∠BAD=40°,且AD=AE,则∠EDC等于 如图,武汉二中广雅中学为了美化学校环境,准备把学校教学楼对面一栋楼房拐角处的空地利用起来.如图,墙PM⊥PN,PM、PN总长15米,在墙角的外侧用36米长的篱笆围起来种花草.要求:AB⊥MP、DE⊥PN、BC⊥AB、CD⊥DE、AB=DE.设AB=x米,凹六边形ABCDEPA的面积为y平方米.
如图,武汉二中广雅中学为了美化学校环境,准备把学校教学楼对面一栋楼房拐角处的空地利用起来.如图,墙PM⊥PN,PM、PN总长15米,在墙角的外侧用36米长的篱笆围起来种花草.要求:AB⊥MP、DE⊥PN、BC⊥AB、CD⊥DE、AB=DE.设AB=x米,凹六边形ABCDEPA的面积为y平方米. 棱长为a的正方体,摆放成如图所示的形状.
棱长为a的正方体,摆放成如图所示的形状.