��Ŀ����
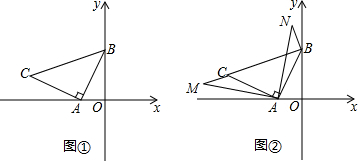
 ��ͼ���人���й�����ѧΪ������ѧУ����������ѧУ��ѧ¥����һ��¥���սǴ��Ŀյ�������������ͼ��ǽPM��PN��PM��PN�ܳ�15�ף���ǽ�ǵ������36�׳������Χ�����ֻ��ݣ�Ҫ��AB��MP��DE��PN��BC��AB��CD��DE��AB=DE����AB=x�ף���������ABCDEPA�����Ϊyƽ���ף�
��ͼ���人���й�����ѧΪ������ѧУ����������ѧУ��ѧ¥����һ��¥���սǴ��Ŀյ�������������ͼ��ǽPM��PN��PM��PN�ܳ�15�ף���ǽ�ǵ������36�׳������Χ�����ֻ��ݣ�Ҫ��AB��MP��DE��PN��BC��AB��CD��DE��AB=DE����AB=x�ף���������ABCDEPA�����Ϊyƽ���ף���1���ú�x�Ĵ���ʽ��ʾAP+PE=
��2����x��ʾy�������x��ȡֵ��Χ��
��3����������ABCDEPA������ܷ�Ϊ105ƽ���ף������ԣ������AB�ij����������ԣ�˵�����ɣ�
���㣺һԪ���η��̵�Ӧ��
ר�⣺����ͼ������
��������1���ӳ�AP��EP�ֱ�CD��BC�ڵ�G��F������AB=x�ף��ó�DE=x�ף�CF=x�ף�CG=x�ף��ٸ���AP+PE=BF+GD������㼴�ɣ�
��2����BF=m�ף���GD=��36-4x-m���ף����ݰ�������ABCDEPA�����y=S�ı���ABFP+S�ı���PGDE+S�ı���PFCG������㼴�ɣ�
��3����-3x2+36x=105���x��ֵ���ٰѲ�������Ľ���ȥ���ɣ�
��2����BF=m�ף���GD=��36-4x-m���ף����ݰ�������ABCDEPA�����y=S�ı���ABFP+S�ı���PGDE+S�ı���PFCG������㼴�ɣ�
��3����-3x2+36x=105���x��ֵ���ٰѲ�������Ľ���ȥ���ɣ�
��� �⣺��1���ӳ�AP��EP�ֱ�CD��BC�ڵ�G��F��
�⣺��1���ӳ�AP��EP�ֱ�CD��BC�ڵ�G��F��
��AB=x�ף�
��AB=DE=x�ף�
��CF=DE=x�ף�CG=AB=x�ף�
��AB+BC+CD+DE+EP+PA=36��
��AP+PE=BF+GD=��36-4x���ף�
�ʴ�Ϊ����36-4x���ף�
��2����BF=m�ף���GD=��36-4x-m���ף�
��������ABCDEPA�����y=S�ı���ABFP+S�ı���PGDE+S�ı���PFCG=mx+x��36-4x-m��+x2=��-3x2+36x����2��
��PM��PN�ܳ�15�ף�
��AP+PE=BF+GD=36-4x��15��
��x��
��
��3����-3x2+36x=105�ã�
x1=5����ȥ����x2=7��
��AB=7�ף�
 �⣺��1���ӳ�AP��EP�ֱ�CD��BC�ڵ�G��F��
�⣺��1���ӳ�AP��EP�ֱ�CD��BC�ڵ�G��F����AB=x�ף�
��AB=DE=x�ף�
��CF=DE=x�ף�CG=AB=x�ף�
��AB+BC+CD+DE+EP+PA=36��
��AP+PE=BF+GD=��36-4x���ף�
�ʴ�Ϊ����36-4x���ף�
��2����BF=m�ף���GD=��36-4x-m���ף�
��������ABCDEPA�����y=S�ı���ABFP+S�ı���PGDE+S�ı���PFCG=mx+x��36-4x-m��+x2=��-3x2+36x����2��
��PM��PN�ܳ�15�ף�
��AP+PE=BF+GD=36-4x��15��
��x��
| 21 |
| 4 |
��3����-3x2+36x=105�ã�
x1=5����ȥ����x2=7��
��AB=7�ף�
���������⿼����һԪ���η��̵�Ӧ�ã��õ���֪ʶ����һԪ���η��̵Ľⷨ�����ε�������ؼ��Ǹ�����֪�������������ߣ���������Σ�

��ϰ��ϵ�д�
�����Ŀ