题目内容
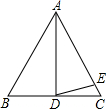如图，在△ABC中，AB=AC，BD=CD，∠BAD=40°，且AD=AE，则∠EDC等于考点：等腰三角形的性质
专题：
分析：由条件可知AD是∠BAC的平分线，则可求得∠DAC，又因为AD=AE，可求得∠ADE，再利用AD⊥DC，可求得∠EDC．
解答：解：∵AB=AC，BD=CD，
∴∠BAD=∠DAC=40°，AD⊥CD，
∵AD=AE，
∴∠ADE=∠AED=
（180°-∠DAE）=
×（180°-40°）=70°，
∴∠EDC=90°-∠ADE=90°-70°=20°，
故答案为：20°．
∴∠BAD=∠DAC=40°，AD⊥CD，
∵AD=AE，
∴∠ADE=∠AED=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EDC=90°-∠ADE=90°-70°=20°，
故答案为：20°．
点评：本题主要考查等腰三角形的性质，掌握等边对等角是解题的关键，注意三角形内角和定理的应用．
练习册系列答案
相关题目
如图，在菱形ABCD中，AE⊥BC，若cos∠B=
如图，AB为⊙O的直径，弦CD⊥AB于点E，若AE=8，BE=2，则AC=