题目内容
11.观察下列等式:(1)32-12=8;(2)52-32=16;(3)72-52=24;(4)92-72=32;…(1)112-92=40.
(2)写出第n个等式(n是正整数):8n.
(3)说明你所写的等式的正确性.
分析 (1)通过观察可发现两个连续奇数的平方差是8的倍数,第n个等式为:(2n+1)2-(2n-1)2=8n,进而求出112-92的值;
(2)由(1)可得第n个等式为:(2n+1)2-(2n-1)2=8n;
(3)原式右边利用平方差公式化简,计算得到结果与左边相等,即可得证.
解答 (1)通过观察可发现两个连续奇数的平方差是8的倍数,
第n个等式为:(2n+1)2-(2n-1)2=8n;
∵2n-1=9,
解得n=5,
∴112-92=8n=5×8=40.
(2)由(1)得:第n个等式为:(2n+1)2-(2n-1)2=8n;
(3)左边=(2n+1+2-1)(2n+1-2n+1)
=4n×2
=8n=右边,
故所写等式正确.
点评 此题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力,本题的关键规律是:(2n+1)2-(2n-1)2=8n.

练习册系列答案
相关题目
19.若分式x2-12(x+1)的值等于0,则x的值为( )
| A. | 1 | B. | ±1 | C. | 12 | D. | -1 |
6.已知不等式组$\left\{\begin{array}{l}{x+8<4x-1}\\{x>m}\end{array}\right.$的解集是x>3,则m的取值范围是( )
| A. | m<3 | B. | m>3 | C. | m≤3 | D. | m≥3 |
3.下列根式中,最简二次根式是( )
| A. | $\sqrt{25a}$ | B. | $\sqrt{{x}^{2}+{y}^{2}}$ | C. | $\sqrt{\frac{a}{2}}$ | D. | $\sqrt{0.7}$ |
1.不等式3|a|-6≤0的整数解为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
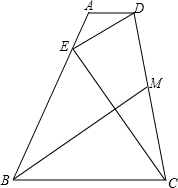 如图,在四边形ABCD中,AD∥BC,AD=AE,BE=BC,连接DE,EC
如图,在四边形ABCD中,AD∥BC,AD=AE,BE=BC,连接DE,EC