题目内容
6.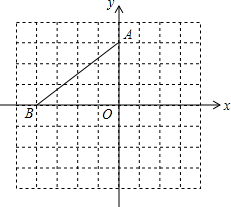 在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F.
在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F.(1)若点B的坐标是(-4,0),请在图中画出△AEF,并写出点E,F的坐标;
(2)点P为x轴上的一个动点,是否存在P使PA+PE的值最小?若不存在,请说明理由,若存在请求出点P的坐标.
分析 (1)根据图形旋转的性质画出△AEF,并写出点E,F的坐标即可;
(2)作点A关于x轴的对称点A′,连接A′E交x轴于点P,则点P即为所求点,利用待定系数法求出直线A′E的解析式,令x=0,求出y的值即可得出P点坐标.
解答  解:(1)如图所示,E(3,3),F(3,-1);
解:(1)如图所示,E(3,3),F(3,-1);
(2)设直线A′E的解析式为y=kx+b(k≠0),
∵A′(0,-3),E(3,3),
∴$\left\{\begin{array}{l}b=-3\\ 3k+b=3\end{array}\right.$,解得k=2,
∴直线A′E的解析式为y=2x-3,
∵当y=0时,x=$\frac{3}{2}$,
∴P($\frac{3}{2}$,0).
点评 本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
15.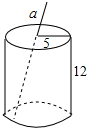 如图是一个圆柱形饮料罐,底面半径为5cm,高为12cm,上底面中心有一个小圆孔,一条长为20cm可到达底部的直吸管在罐外部分a长度(罐壁厚度和小圆孔大小忽略不计)范围是( )
如图是一个圆柱形饮料罐,底面半径为5cm,高为12cm,上底面中心有一个小圆孔,一条长为20cm可到达底部的直吸管在罐外部分a长度(罐壁厚度和小圆孔大小忽略不计)范围是( )
 如图是一个圆柱形饮料罐,底面半径为5cm,高为12cm,上底面中心有一个小圆孔,一条长为20cm可到达底部的直吸管在罐外部分a长度(罐壁厚度和小圆孔大小忽略不计)范围是( )
如图是一个圆柱形饮料罐,底面半径为5cm,高为12cm,上底面中心有一个小圆孔,一条长为20cm可到达底部的直吸管在罐外部分a长度(罐壁厚度和小圆孔大小忽略不计)范围是( )| A. | 8≤a≤15 | B. | 5≤a≤8 | C. | 7≤a≤8 | D. | 7≤a≤15 |
 为了方便行人推车过天桥,某相关部门在10m高的天桥两端修建了40m长的斜道(如图),求这条斜道的坡角α(精确到1′).
为了方便行人推车过天桥,某相关部门在10m高的天桥两端修建了40m长的斜道(如图),求这条斜道的坡角α(精确到1′).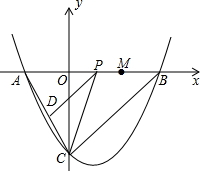 已知:如图,抛物线y=a(x-1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(-2,0).
已知:如图,抛物线y=a(x-1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(-2,0).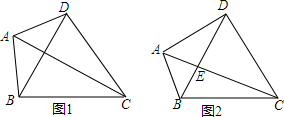
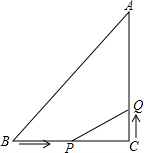 如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s速度向点c移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s速度向点c移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t. 如图为y=-2x2+bx+c的图象
如图为y=-2x2+bx+c的图象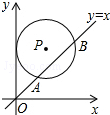 如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{5}$,则a的值是2$\sqrt{2}$+3.
如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{5}$,则a的值是2$\sqrt{2}$+3.