题目内容
14.计算:$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{10}+\sqrt{9}}$=$\sqrt{10}$-1.分析 首先利用二次根式的性质,结合分母有理化进而求出答案.
解答 解:$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{10}+\sqrt{9}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{10}$-$\sqrt{9}$
=$\sqrt{10}$-1.
故答案为:$\sqrt{10}$-1.
点评 此题主要考查了分母有理化,正确找出有理化因式是解题关键.

练习册系列答案
相关题目
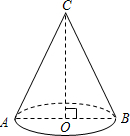 如图所示,圆锥形漏斗的侧面积为60π,它的底面半径OB=6cm,则这个圆锥形漏斗的高OC是8cm.
如图所示,圆锥形漏斗的侧面积为60π,它的底面半径OB=6cm,则这个圆锥形漏斗的高OC是8cm.
 已知:∠AOB=60°,∠B0C=30°,OE是∠AOB平分线,求∠COE度数.
已知:∠AOB=60°,∠B0C=30°,OE是∠AOB平分线,求∠COE度数.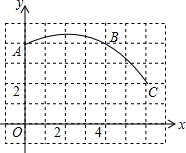 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作: