题目内容
15.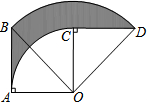 如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.
如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.
分析 根据旋转的性质得到AO=CO=2,BO=DO=2$\sqrt{2}$,然后根据阴影部分面积=S扇形OBD+S△AOB-S扇形OAC-S△COD=S扇形OBD-S扇形OAC,代入数值即可得到结果.
解答 解:∵Rt△OAB中,∠AOB=45°,AB=2,
∴AO=2,BO=2$\sqrt{2}$,
∵将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,
∴CO=OA=2,DO=OB=2$\sqrt{2}$,
∴阴影部分面积=S扇形OBD+S△AOB-S扇形OAC-S△COD=S扇形OBD-S扇形OAC=$\frac{90•π×(2\sqrt{2})^{2}}{360}$-$\frac{90•π×{2}^{2}}{360}$=π,
故答案为:π.
点评 本题考查了解直角三角形,旋转的性质,扇形的面积公式,熟记扇形的面积公式是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
5. 如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )
如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )
 如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )
如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )| A. | 45° | B. | 60° | C. | 90° | D. | 180° |
6.若(x1,y1)(x2,y2)都是y=-$\frac{5}{x}$的图象上的点,且x1<x2<0,则下列各式正确的是( )
| A. | y1>y2>0 | B. | y1<y2<0 | C. | y2>y1>0 | D. | y2<0<y1 |
5.下列事件中最适合使用普查方式收集数据的是( )
| A. | 了解某班同学的体重情况 | B. | 了解我省初中学生的兴趣爱好情况 | ||
| C. | 了解一批电灯泡的使用寿命 | D. | 了解我省农民工的年收入情况 |
 在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).
在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).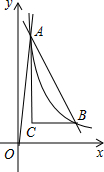 如图,在平面直角坐标系xOy中,正比例函数y=10x与反比例函数y=$\frac{k}{x}$交于点A,点A的横坐标为$\frac{1}{2}$,反比例函数y=$\frac{k}{x}$图象上有一点B,过点B作BC∥x轴,过点A作AC⊥BC,垂足为点C.
如图,在平面直角坐标系xOy中,正比例函数y=10x与反比例函数y=$\frac{k}{x}$交于点A,点A的横坐标为$\frac{1}{2}$,反比例函数y=$\frac{k}{x}$图象上有一点B,过点B作BC∥x轴,过点A作AC⊥BC,垂足为点C.