题目内容
20.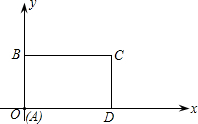 如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.(1)求P点从A点运动到D点所需的时间;
(2)设P点的运动时间为t(秒),
①当t=8时,求出点P的坐标;
②若△OAP面积为S,试探究点P在运动过程中S与t之间的关系式.
分析 (1)求出AB+BC+CD即可得出结论;
(2)①先判断出先P在边BC上,向右移动的单位数,再确定出矩形向右平移的单位数即可得出结论;
②分三种情况利用三角形的面积公式即可求解.
解答 解:(1)P点从A点运动到D点所需的时间=(3+6+3)÷1=12(秒)
(2)①当t=8时,P点从A点运动到边BC上,
如图,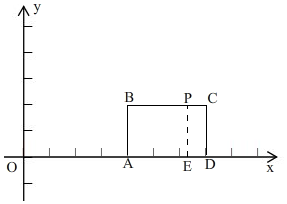
过点P作PE⊥AD于点E.
此时A点到E点的时间=8秒,AB+BP=8,
∴BP=5,则PE=AB=3,AE=BP=5
∵矩形向右移动2×8=16
∴OE=OA+AE=16+5=21
∴点P的坐标为(21,3).
②分三种情况:
Ⅰ、0<t≤3时,点P在AB上运动,此时OA=2t,AP=t
∴s=$\frac{1}{2}$×2t×t=t2
Ⅱ、3<t≤9时,点P在BC上运动,此时OA=2t
∴s=$\frac{1}{2}$×2t×3=3t
Ⅲ、9<t<12时,点P在CD上运动,此时OA=2t,AB+BC+CP=t
∴DP=(AB+BC+CD)-(AB+BC+CP)=12-t
∴s=$\frac{1}{2}$×2t×(12-t)=-t2+12t
综上所述,s与t之间的函数关系式是:s=$\left\{\begin{array}{l}{{t}^{2}(0<t≤3)}\\{3t(3<t≤9)}\\{-{t}^{2}+12t(9<t≤12)}\end{array}\right.$.
点评 此题是四边形综合题,主要考查了平移的特点,三角形的面积公式,解本题的关键是(2)②分类讨论的思想解决问题,是一道比较简单的中考常考题.

练习册系列答案
相关题目
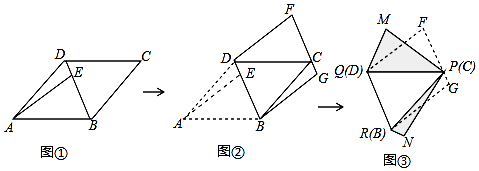
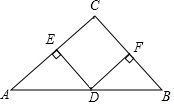 如图,△ABC中,∠C=90°,AC=BC,点D是AB的中点,分别过点D作DE⊥AC,DF⊥BC,垂足分别为点E,F,求证:四边形CEDF是正方形.
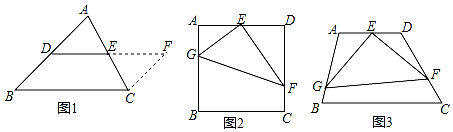
如图,△ABC中,∠C=90°,AC=BC,点D是AB的中点,分别过点D作DE⊥AC,DF⊥BC,垂足分别为点E,F,求证:四边形CEDF是正方形.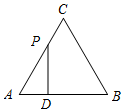 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )
如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )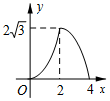
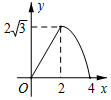
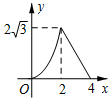
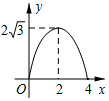
 如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ACB、∠DCB、∠EDC的度数.
如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ACB、∠DCB、∠EDC的度数.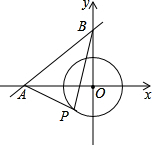 如图,直线y=$\frac{3}{4}$+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为11cm2.
如图,直线y=$\frac{3}{4}$+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为11cm2.