题目内容
10.若$\sqrt{-\frac{a}{a+1}}$=$\frac{\sqrt{-a}}{\sqrt{a+1}}$成立,则a的取值范围是-1<a≤0.分析 直接利用二次根式的性质化简求出a的取值范围.
解答 解:∵$\sqrt{-\frac{a}{a+1}}$=$\frac{\sqrt{-a}}{\sqrt{a+1}}$成立,
∴$\left\{\begin{array}{l}{-a≥0}\\{a+1>0}\end{array}\right.$,
解得:-1<a≤0.
故答案为:-1<a≤0.
点评 此题主要考查了二次根式的性质,正确把握二次根式的性质是解题关键.

练习册系列答案
相关题目
20.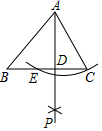 如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )
如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )
 如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )
如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
15.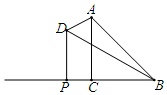 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )| A. | 一直变大 | B. | 一直变小 | C. | 先变小再变大 | D. | 先变大再变小 |
2.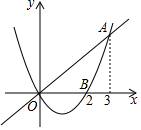 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | x<0或x>3 | C. | 2<x<3 | D. | 0<x<3 |
 如图是某校参加各兴趣小组的学生人数分布扇形统计图,其中“演艺”兴趣小组一项所对应的角度是108°.
如图是某校参加各兴趣小组的学生人数分布扇形统计图,其中“演艺”兴趣小组一项所对应的角度是108°.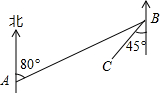 一艘轮船从点A出发沿北偏东80°,方向航行到点B后再沿西南方向航行,则∠ABC=35°.
一艘轮船从点A出发沿北偏东80°,方向航行到点B后再沿西南方向航行,则∠ABC=35°.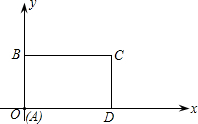 如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.