题目内容
15.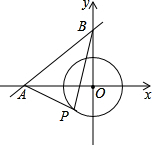 如图,直线y=$\frac{3}{4}$+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为11cm2.
如图,直线y=$\frac{3}{4}$+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为11cm2.
分析 先求出OA,OB,进而求出AB,再判断出△PAB的AB边上的高最大时必过⊙O的圆心O,最后利用面积求出OC即可得出CP即可.
解答 解:如图,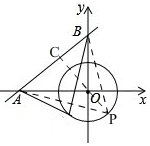
∵直线y=$\frac{3}{4}$+3与坐标轴交于A、B两点,
∴A(-4,0),B(0,3),
∴OA=4,OB=3,
在Rt△AOB中,根据勾股定理得,AB=5,
∵△PAB中,AB=5是定值,
∴要使△PAB的面积最大,即⊙O上的点到AB的距离最大,
∴过点O作OC⊥AB于C,CO的延长线交⊙O于P,此时S△PAB的面积最大,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OC,
∴OC=$\frac{OA•OB}{AB}$=$\frac{4×3}{5}$=$\frac{12}{5}$,
∵⊙O的半径为2,
∴CP=OC+OP=$\frac{22}{5}$,
∴S△PAB=$\frac{1}{2}$AB•CP=$\frac{1}{2}$×5×$\frac{22}{5}$=11.
故答案为11.
点评 此题考查了圆的性质,圆中最大的弦,一次函数图象上点的坐标特征,解本题的关键是确定出三角形PAB的AB边上的高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.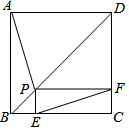 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=$\sqrt{2}$EC.其中正确结论的番号是( )
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=$\sqrt{2}$EC.其中正确结论的番号是( )
 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=$\sqrt{2}$EC.其中正确结论的番号是( )
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=$\sqrt{2}$EC.其中正确结论的番号是( )| A. | ①②④⑤ | B. | ①②③④⑤ | C. | ①②④ | D. | ①④ |
5. 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )| A. | 15° | B. | 20° | C. | 30° | D. | 25° |
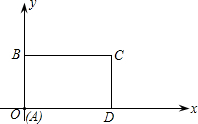 如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.