题目内容
12．
如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠ACB、∠DCB、∠EDC的度数．
分析 根据两直线平行，同位角相等，内错角相等进行判断即可．
解答 解：∵DE∥BC，
∴∠ACB=∠AED=80°，
∵CD平分∠ACB，
∴∠DCB=$\frac{1}{2}$∠ACB=40°，
∵DE∥BC，
∴∠EDC=∠DCB=40°．
点评 本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等，两直线平行，内错角相等．
练习册系列答案
相关题目
2．
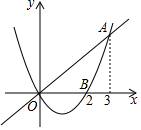如图，已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A（3，2），与x轴交于点B（2，0），若y1＜y2，则x的取值范围是（ ）
如图，已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A（3，2），与x轴交于点B（2，0），若y1＜y2，则x的取值范围是（ ）| A． | 0＜x＜2 | B． | x＜0或x＞3 | C． | 2＜x＜3 | D． | 0＜x＜3 |
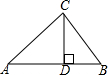某校把一块形状为直角三角形的废地开辟为生物园，如图所示，∠ACB=90°，AC=80米，BC=60米，若线段CD是一条小渠，且D点在边AB上，已知水果的造价为30元/米，问D点在距A点多远处时，水渠的造价最低？最低造价是多少？
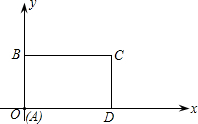如图所示，在平面直角坐标系中，矩形ABCD的边AD在x轴上，点A在原点，AB=3，AD=6．若矩形以每秒2个单位长度沿x轴正方向作匀速运动．同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动，当P点运动到D点时停止运动，矩形ABCD也随之停止运动．
7．
6张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）
6张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）| A． | a=2b | B． | a=3b | C． | a=4b | D． | a=b |
细心观察图，认真分析各式，然后解答问题：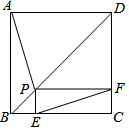
如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=$\sqrt{2}$EC．其中正确结论的番号是（ ）