题目内容
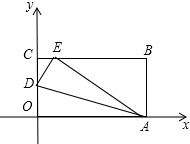 如图,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12.
如图,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12.(1)矩形OABC的周长为
(2)若A点坐标为(5,0),求线段AE所在直线的解析式.
考点:一次函数综合题
专题:
分析:(1)根据折叠和矩形的性质得出AE=OA=BC,OD=DE,BC=OA,AB=OC,根据已知得出CE+CD+DE+AB+BE+AE=16,推出CE+BE+AB+OA+OD+CD=16即可.
(2)根据勾股定理求出BE,求出CE,再利用待定系数法求出直线AE的解析式即可.
(2)根据勾股定理求出BE,求出CE,再利用待定系数法求出直线AE的解析式即可.
解答:解:(1)∵以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,四边形OABC是矩形,
∴AE=OA=BC,OD=DE,BC=OA,AB=OC,
∵△ECD的周长为4,△EBA的周长为12,
∴CE+CD+DE+AB+BE+AE=4+12=16,
∴CE+BE+AB+OA+OD+CD=16,
即矩形OABC的周长为16,
故答案为:16.
(2)∵矩形OABC的周长为16,
∴2OA+2OC=16,
∵A点坐标为(5,0),
∴OA=5,
∴OC=3,
∵在Rt△ABE中,∠B=90°,AB=3,AE=OA=5,由勾股定理得:BE=4,
∴CE=5-4=1,
∴E的坐标是(1,3).
设直线AE的解析式为y=kx+b(k≠0),
∵A(5,0),E(1,3),
∴
,
解得
.
∴线段AE所在直线的解析式为:y=-
x+
.
∴AE=OA=BC,OD=DE,BC=OA,AB=OC,
∵△ECD的周长为4,△EBA的周长为12,
∴CE+CD+DE+AB+BE+AE=4+12=16,
∴CE+BE+AB+OA+OD+CD=16,
即矩形OABC的周长为16,
故答案为:16.
(2)∵矩形OABC的周长为16,
∴2OA+2OC=16,
∵A点坐标为(5,0),
∴OA=5,
∴OC=3,
∵在Rt△ABE中,∠B=90°,AB=3,AE=OA=5,由勾股定理得:BE=4,
∴CE=5-4=1,
∴E的坐标是(1,3).
设直线AE的解析式为y=kx+b(k≠0),
∵A(5,0),E(1,3),
∴
|
解得
|
∴线段AE所在直线的解析式为:y=-
| 3 |
| 4 |
| 15 |
| 4 |
点评:本题考查的是一次函数综合题,涉及到勾股定理,矩形的性质,折叠的性质的应用,难度适中.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
下列说法正确的是( )
| A、0.1是0.01的算术平方根 | ||
| B、0.6是3.6的算术平方根 | ||
C、3是
| ||
| D、-2是(-2)2的算术平方根 |
 如图,有一块矩形铁皮,长100cm,宽50cm,在它的四角各切去一个同样大小的正方形,然后将四周突出部分折起,就能制作成一个无盖的方盒,如果制成的无盖方盒的底面积为3600cm2,那么制成的方盒的体积是多少cm3?
如图,有一块矩形铁皮,长100cm,宽50cm,在它的四角各切去一个同样大小的正方形,然后将四周突出部分折起,就能制作成一个无盖的方盒,如果制成的无盖方盒的底面积为3600cm2,那么制成的方盒的体积是多少cm3? 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,求点C的坐标和周长.
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,求点C的坐标和周长.