题目内容
13.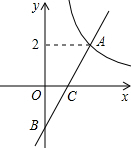 已知,在平面直角坐标系xOy中,函数y=$\frac{4}{x}$(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).
已知,在平面直角坐标系xOy中,函数y=$\frac{4}{x}$(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,若P是x轴上一点,且满足△PAB的面积是6,求点P的坐标.
分析 (1)将A点坐标代入y=$\frac{4}{x}$(x>0),求出m的值为2,再将(2,2)代入y=kx-k,求出k的值,即可得到一次函数的解析式;
(2)将三角形以x轴为分界线,分为两个三角形计算,再把它们相加.
解答 解:(1)根据题意,将点A(m,2)代入y=$\frac{4}{x}$,
得:2=$\frac{4}{m}$,
解得:m=2,
即点A(2,2),
将点A(2,2)代入y=kx-k,得:2=2k-k,
解得:k=2,
∴一次函数的解析式为y=2x-2;
(2)如图,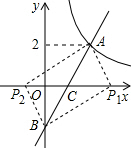
∵一次函数y=2x-2与x轴的交点为C(1,0),与y轴的交点为B(0,-2),
S△ABP=S△ACP+S△BPC,
∴$\frac{1}{2}$×2CP+$\frac{1}{2}$×2CP=6,
解得CP=3,
则P点坐标为(4,0),(-2,0).
点评 本题考查了反比例函数与一次函数的交点问题,求出函数解析式并熟悉点的坐标与图形的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.如果将抛物线y=(x-1)2+2向下平移1个单位,那么所得的抛物线解析式是( )
| A. | y=(x-1)2+3 | B. | y=(x-1)2+1 | C. | y=(x-2)2+2 | D. | y=x2+2 |
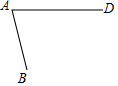 如图是一个还未画好的中心对称图形,它是一个四边形ABCD,其中A与C,B与D是对称点.
如图是一个还未画好的中心对称图形,它是一个四边形ABCD,其中A与C,B与D是对称点.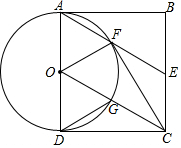 如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.
如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.