题目内容
2.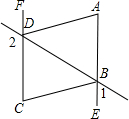 已知:如图,∠1+∠2=180°,AD∥BC,DA平分∠BDF,
已知:如图,∠1+∠2=180°,AD∥BC,DA平分∠BDF,(1)试判断直线AE与CF有怎样的位置关系?并说明理由;
(2)BC平分∠DBE吗?为什么?
分析 (1)根据已知求出∠CDB=∠ABD,根据平行线的判定推出即可;
(2)根据平行线的性质得出∠FDB=∠EBD,∠ADB=∠CBD,根据角平分线定义得出∠FDB=2∠ADB,求出∠EBD=2∠CBD,即可得出答案.
解答 解:(1)AE∥CF,
理由是:∵∠2+∠CDB=180°,∠1=∠ABD,∠1+∠2=180°,
∴∠CDB=∠ABD,
∴AE∥CF;
(2)BC平分∠DBE,
理由是:∵CF∥AE,AD∥BC,
∴∠FDB=∠EBD,∠ADB=∠CBD,
∵DA平分∠ADB,
∴∠FDB=2∠ADB,
∴∠EBD=2∠CBD,
即∠CBD=∠EBC,
∴BC平分∠DBE.
点评 本题考查了角平分线定义,平行线的性质和判定的应用,能运用定理进行推理是解此题的关键,注意:两直线平行,内错角相等,反之亦然.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
7.下列计算正确的是( )
| A. | 2t-t=2 | B. | t2•t3=t6 | C. | (-t2)3=-t5 | D. | t3÷t2=t |
11.一元一次不等式组$\left\{\begin{array}{l}{2x-1<3}\\{x+3>2x}\end{array}\right.$的解是( )
| A. | -2<x<3 | B. | -3<x<2 | C. | x<-3 | D. | x<2 |
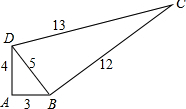 一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?求出四边形ABCD的面积.
一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?求出四边形ABCD的面积.